
Intersection form (4-manifold)
Encyclopedia
In mathematics
, the intersection form of an oriented compact 4-manifold
is a special symmetric bilinear form on the 2nd cohomology group of the 4-manifold. It reflects much of the topology of the 4-manifolds, including information on the existence of a smooth structure
.

is given by
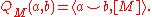
When the 4-manifold is also smooth, then in de Rham cohomology
, if a and b are represented by 2-forms α and β, then the intersection form can be expressed by the integral
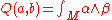
where is the wedge product, see exterior algebra
is the wedge product, see exterior algebra
.
allows a geometric definition of the intersection form. If the Poincaré duals of a and b are represented by surfaces (or 2-cocycles) A and B meeting transversely, then each intersection point has a multipicity +1 or −1 depending on the orientations, and QM(a, b) is the sum of these multiplicities.
Thus the intersection form can also be thought of as a pairing on the 2nd homology group. Poincare duality also implies that the form is unimodular
(up to torsion).
4-manifold must have even intersection form, i.e. Q(x,x) is even for every x. For a simply-connected 4-manifold (or more generally one with no 2-torsion residing in the first homology), the converse holds.
The signature of the intersection form is an important invariant. A 4-manifold bounds a 5-manifold if and only if it has zero signature. Van der Blij's lemma implies that a spin 4-manifold has signature a multiple of eight. In fact, Rokhlin's theorem
implies that a smooth compact spin 4-manifold has signature a multiple of 16.
Michael Freedman
used the intersection form to classify simply-connected topological 4-manifolds. Given any unimodular symmetric bilinear form over the integers, Q, there is a simply-connected closed 4-manifold M with intersection form Q. If Q is even, there is only one such manifold. If Q is odd, there are two, with at least one (possibly both) having no smooth structure. Thus two simply-connected closed smooth 4-manifolds with the same intersection form are homeomorphic. In the odd case, the two manifolds are distinguished by their Kirby–Siebenmann invariant.
Donaldson's theorem
states a smooth simply-connected 4-manifold with positive definite intersection form has the diagonal (scalar 1) intersection form. So Freedman's classification implies there are many non-smoothable 4-manifolds, for example the E8 manifold
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the intersection form of an oriented compact 4-manifold
4-manifold
In mathematics, 4-manifold is a 4-dimensional topological manifold. A smooth 4-manifold is a 4-manifold with a smooth structure. In dimension four, in marked contrast with lower dimensions, topological and smooth manifolds are quite different...
is a special symmetric bilinear form on the 2nd cohomology group of the 4-manifold. It reflects much of the topology of the 4-manifolds, including information on the existence of a smooth structure
Smooth structure
In mathematics, a smooth structure on a manifold allows for an unambiguous notion of smooth function. In particular, a smooth structure allows one to perform mathematical analysis on the manifold....
.
Definition
The intersection form
is given by
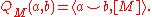
When the 4-manifold is also smooth, then in de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
, if a and b are represented by 2-forms α and β, then the intersection form can be expressed by the integral
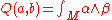
where
 is the wedge product, see exterior algebra
is the wedge product, see exterior algebraExterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
.
Poincaré duality
Poincaré dualityPoincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
allows a geometric definition of the intersection form. If the Poincaré duals of a and b are represented by surfaces (or 2-cocycles) A and B meeting transversely, then each intersection point has a multipicity +1 or −1 depending on the orientations, and QM(a, b) is the sum of these multiplicities.
Thus the intersection form can also be thought of as a pairing on the 2nd homology group. Poincare duality also implies that the form is unimodular
Unimodular form
In mathematics, in the module theory of a commutative ring, a bilinear form on a module V is unimodular if it induces an isomorphismV \to V^*.Here V^* denotes the dual module of V....
(up to torsion).
Properties and applications
By Wu's formula, a spinSpin structure
In differential geometry, a spin structure on an orientable Riemannian manifold \,allows one to define associated spinor bundles, giving rise to the notion of a spinor in differential geometry....
4-manifold must have even intersection form, i.e. Q(x,x) is even for every x. For a simply-connected 4-manifold (or more generally one with no 2-torsion residing in the first homology), the converse holds.
The signature of the intersection form is an important invariant. A 4-manifold bounds a 5-manifold if and only if it has zero signature. Van der Blij's lemma implies that a spin 4-manifold has signature a multiple of eight. In fact, Rokhlin's theorem
Rokhlin's theorem
In 4-dimensional topology, a branch of mathematics, Rokhlin's theorem states that if a smooth, compact 4-manifold M has a spin structure , then the signature of its intersection form, a quadratic form on the second cohomology group H2, is divisible by 16...
implies that a smooth compact spin 4-manifold has signature a multiple of 16.
Michael Freedman
Michael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
used the intersection form to classify simply-connected topological 4-manifolds. Given any unimodular symmetric bilinear form over the integers, Q, there is a simply-connected closed 4-manifold M with intersection form Q. If Q is even, there is only one such manifold. If Q is odd, there are two, with at least one (possibly both) having no smooth structure. Thus two simply-connected closed smooth 4-manifolds with the same intersection form are homeomorphic. In the odd case, the two manifolds are distinguished by their Kirby–Siebenmann invariant.
Donaldson's theorem
Donaldson's theorem
In mathematics, Donaldson's theorem states that a definite intersection form of a simply connected smooth manifold of dimension 4 is diagonalisable. If the intersection form is positive definite, it can be diagonalized to the identity matrix...
states a smooth simply-connected 4-manifold with positive definite intersection form has the diagonal (scalar 1) intersection form. So Freedman's classification implies there are many non-smoothable 4-manifolds, for example the E8 manifold
E8 manifold
In mathematics, the E8 manifold is the unique compact, simply connected topological 4-manifold with intersection form the E8 lattice.The E8 manifold was discovered by Michael Freedman in 1982...
.

