
Integrated Encryption Scheme
Encyclopedia
Integrated Encryption Scheme (IES) is a hybrid encryption scheme which provides semantic security
against an adversary
who is allowed to use chosen-plaintext and chosen-ciphertext attacks. The security of the scheme is based on the Diffie–Hellman problem. Two incarnations of the IES are standardized: Discrete Logarithm
Integrated Encryption Scheme (DLIES) and Elliptic Curve
Integrated Encryption Scheme (ECIES), which is also known as the Elliptic Curve Augmented Encryption Scheme or simply the Elliptic Curve Encryption Scheme. These two incarnations are identical up to the change of an underlying group and so to be concrete we concentrate on the latter.
To send an encrypted message to Bob
using ECIES Alice needs the following information:
To encrypt a message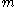 Alice does the following:
Alice does the following:
To decrypt the ciphertext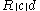 Bob does the following:
Bob does the following:
Semantic security
Semantic security is a widely used definition for security in an asymmetric key encryption algorithm. For a cryptosystem to be semantically secure, it must be infeasible for a computationally bounded adversary to derive significant information about a message when given only its ciphertext and...
against an adversary
Adversary (cryptography)
In cryptography, an adversary is a malicious entity whose aim is to prevent the users of the cryptosystem from achieving their goal...
who is allowed to use chosen-plaintext and chosen-ciphertext attacks. The security of the scheme is based on the Diffie–Hellman problem. Two incarnations of the IES are standardized: Discrete Logarithm
Discrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
Integrated Encryption Scheme (DLIES) and Elliptic Curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
Integrated Encryption Scheme (ECIES), which is also known as the Elliptic Curve Augmented Encryption Scheme or simply the Elliptic Curve Encryption Scheme. These two incarnations are identical up to the change of an underlying group and so to be concrete we concentrate on the latter.
To send an encrypted message to Bob
Alice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
using ECIES Alice needs the following information:
- cryptographic suite to be used:
- KDFKey derivation functionIn cryptography, a key derivation function derives one or more secret keys from a secret value such as a master key or other known information such as a password or passphrase using a pseudo-random function...
, e.g., ANSI-X9.63-KDF with SHA-1 option; - MACMessage authentication codeIn cryptography, a message authentication code is a short piece of information used to authenticate a message.A MAC algorithm, sometimes called a keyed hash function, accepts as input a secret key and an arbitrary-length message to be authenticated, and outputs a MAC...
, e.g., HMAC-SHA-1-160 with 160-bit keys or HMAC-SHA-1-80 with 80-bit keys; - symmetric encryption schemeSymmetric-key algorithmSymmetric-key algorithms are a class of algorithms for cryptography that use trivially related, often identical, cryptographic keys for both encryption of plaintext and decryption of ciphertext. The encryption key is trivially related to the decryption key, in that they may be identical or there is...
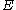 , e.g., TDEA in CBC mode or XOR encryption scheme;
, e.g., TDEA in CBC mode or XOR encryption scheme;
- KDF
- EC domain parameters:
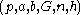 for a curve over prime field or
for a curve over prime field or 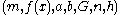 for a curve over binary field;
for a curve over binary field; - Bob's public key:
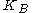 (Bob generates it as follows:
(Bob generates it as follows: 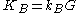 , where
, where 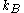 is the private key he chooses at random:
is the private key he chooses at random: 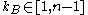 );
); - optional shared information:
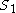 and
and 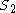 .
.
To encrypt a message
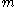 Alice does the following:
Alice does the following:
- generates a random number
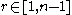 and calculates
and calculates 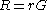 ;
; - derives a shared secret:
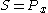 , where
, where 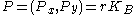 (and
(and 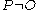 );
); - uses KDF to derive a symmetric encryption and a MAC keys:
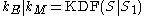 ;
; - encrypts the message:
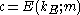 ;
; - computes the tag of encrypted message and
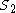 :
: 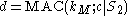 ;
; - outputs
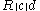 .
.
To decrypt the ciphertext
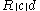 Bob does the following:
Bob does the following:
- derives the shared secret:
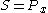 , where
, where 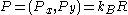 (it is the same as the one Alice derived because
(it is the same as the one Alice derived because 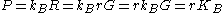 ), or outputs failed if
), or outputs failed if 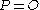 ;
; - derives keys the same way as Alice did:
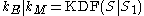 ;
; - uses MAC to check the tag and outputs failed if
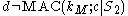 ;
; - uses symmetric encryption scheme to decrypt the message
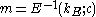 .
.

