
Identifiability
Encyclopedia
In statistics
, identifiability is a property which a model
must satisfy in order for inference
to be possible. We say that the model is identifiable if it is theoretically possible to learn the true value of this model’s underlying parameter after obtaining an infinite number of observations from it. Mathematically, this is equivalent to saying that different values of the parameter must generate different probability distribution
s of the observable variables. Usually the model is identifiable only under certain technical restrictions, in which case the set of these requirements is called the identification conditions.
In some cases, the model is unidentifiable, but it is still possible to learn the true values of a certain subset of the model parameters. In this case we say that the model is partially identifiable. In other cases it may be possible to learn the location of the true parameter up to a certain finite region of the parameter space, in which case the model is set identifiable.
where the parameter space Θ is either finite- or infinite-dimensional. We say that ℘ is identifiable if the mapping θ ↦ Pθ is one-to-one:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, identifiability is a property which a model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
must satisfy in order for inference
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
to be possible. We say that the model is identifiable if it is theoretically possible to learn the true value of this model’s underlying parameter after obtaining an infinite number of observations from it. Mathematically, this is equivalent to saying that different values of the parameter must generate different probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s of the observable variables. Usually the model is identifiable only under certain technical restrictions, in which case the set of these requirements is called the identification conditions.
In some cases, the model is unidentifiable, but it is still possible to learn the true values of a certain subset of the model parameters. In this case we say that the model is partially identifiable. In other cases it may be possible to learn the location of the true parameter up to a certain finite region of the parameter space, in which case the model is set identifiable.
Definition
Let ℘ = {Pθ: θ∈Θ} be a statistical modelStatistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
where the parameter space Θ is either finite- or infinite-dimensional. We say that ℘ is identifiable if the mapping θ ↦ Pθ is one-to-one:
-

This definition means that distinct values of θ should correspond to distinct probability distributions: if θ1≠θ2, then also Pθ1≠Pθ2. If the distributions are defined in terms of the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s, then two pdfs should be considered distinct only if they differ on a set of non-zero measure (for example two functions ƒ1(x)=10≤x<1 and ƒ2(x)=10≤x≤1 differ only at a single point x=1 — a set of measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero — and thus cannot be considered as distinct pdfs).
Identifiability of the model in the sense of invertibility of the map θ ↦ Pθ is equivalent to being able to learn the model’s true parameter if the model can be observed indefinitely long. Indeed, if {Xt}⊆S is the sequence of observations from the model, then by the strong law of large numbers,-
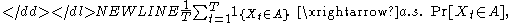
for every measurable set A⊆S (here 1{…} is the indicator function). Thus with an infinite number of observations we will be able to find the true probability distribution P0 in the model, and since the identifiability condition above requires that the map θ ↦ Pθ be invertible, we will also be able to find the true value of the parameter which generated given distribution P0.
Example 1
Let ℘ be the normal location-scale familyLocation-scale familyIn probability theory, especially as that field is used in statistics, a location-scale family is a family of univariate probability distributions parametrized by a location parameter and a non-negative scale parameter; if X is any random variable whose probability distribution belongs to such a...
:-
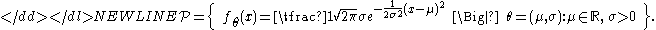
Then-
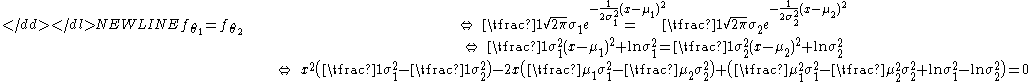
This expression is equal to zero for almost all x only when all its coefficients are equal to zero, which is only possible when |σ1| = |σ2| and μ1 = μ2. Since in the scale parameter σ is restricted to be greater than zero, we conclude that the model is identifiable: ƒθ1=ƒθ2 ⇔ θ1=θ2.
Example 2
Let ℘ be the standard linear regression model:-
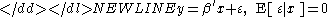
(where ′ denotes matrix transposeTransposeIn linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
). Then the parameter β is identifiable if and only if the matrix E[xx′] is invertible. Thus, this is the identification condition in the model.
Example 3
Suppose ℘ is the classical errors-in-variables linear modelLinear modelIn statistics, the term linear model is used in different ways according to the context. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However the term is also used in time series analysis with a different...
:-

where (ε,η,x*) are jointly normal independent random variables with zero expected value and unknown variances, and only the variables (x,y) are observed. Then this model is not identifiable, only the product βσ²∗ is (where σ²∗ is the variance of the latent regressor x*). This is also an example of set identifiable model: although the exact value of β cannot be learned, we can guarantee that it must lie somewhere in the interval (βyx, 1÷βxy), where βyx is the coefficient in OLSOrdinary least squaresIn statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
regression of y on x, and βxy is the coefficient in OLS regression of x on y.
If we abandon the normality assumption and require that x* were not normally distributed, retaining only the independence condition ε⊥η⊥x*, then the model becomes identifiable.
Software
In the case of parameter estimation in partially observed dynamical systems, the profile likelihood can be also used for structural and practical identifiability analysis. An implementation of the Profile Likelihood Approach is available in the MATLAB Toolbox PottersWheelPottersWheelPottersWheel is a MATLAB toolbox for mathematical modeling of time-dependent dynamical systems that can be expressed as chemical reaction networks or ordinary differential equations . It allows the automatic calibration of model parameters by fitting the model to experimental measurements...
.
-
-
-
-
-

