Hybrid Monte Carlo
Encyclopedia
In mathematics
and physics
, the Hybrid Monte Carlo algorithm, also known as Hamiltonian Monte Carlo, is a Markov chain Monte Carlo
method for obtaining a sequence of random samples
from a probability distribution
for which direct sampling is difficult. This sequence can be used to approximate the distribution (i.e., to generate a histogram), or to compute an integral
(such as an expected value
).
It differs from the Metropolis–Hastings algorithm by reducing the correlation between successive states sampled by using a Hamiltonian
evolution between states and additionally by targeting states with a higher acceptance criteria the observed probability distribution converges more quickly to the absolute probability distribution. It was devised by Simon Duane, A.D. Kennedy, Brian Pendleton and Duncan Roweth in 1987. It proposes a state based on an arbitrary choose function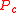
, which dictates the probability of choosing any state 
and then accepts or rejects the proposed state with probability 
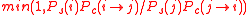, this acceptance criteria has the convenient property of maintaining detailed balance
for any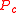
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Hybrid Monte Carlo algorithm, also known as Hamiltonian Monte Carlo, is a Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
method for obtaining a sequence of random samples
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
from a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
for which direct sampling is difficult. This sequence can be used to approximate the distribution (i.e., to generate a histogram), or to compute an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
(such as an expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
).
It differs from the Metropolis–Hastings algorithm by reducing the correlation between successive states sampled by using a Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
evolution between states and additionally by targeting states with a higher acceptance criteria the observed probability distribution converges more quickly to the absolute probability distribution. It was devised by Simon Duane, A.D. Kennedy, Brian Pendleton and Duncan Roweth in 1987. It proposes a state based on an arbitrary choose function
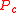, which dictates the probability of choosing any state and then accepts or rejects the proposed state with probability 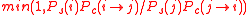, this acceptance criteria has the convenient property of maintaining detailed balanceDetailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
for any
.
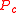