
Hurwitz's theorem (complex analysis)
Encyclopedia
In complex analysis
, a field within mathematics, Hurwitz's theorem, named after Adolf Hurwitz
, roughly states that, under certain conditions, if a sequence
of holomorphic function
s converges uniformly to a holomorphic function on compact sets, then after a while those functions and the limit function have the same number of zeros
in any open disk.
More precisely, let be an open set
be an open set
in the complex plane
, and consider a sequence of holomorphic functions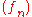 which converges uniformly on compact subsets of
which converges uniformly on compact subsets of  to a holomorphic function
to a holomorphic function 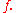 Let
Let  be an open disk of center
be an open disk of center  and radius
and radius  which is contained in
which is contained in  together with its boundary
together with its boundary
. Assume that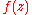 has no zeros on the disk boundary. Then, there exists a natural number
has no zeros on the disk boundary. Then, there exists a natural number
 such that for all
such that for all  greater than
greater than  the functions
the functions 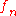 and
and  have the same number of zeros in
have the same number of zeros in 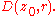
The requirement that have no zeros on the disk boundary is necessary. For example, consider the unit disk, and the sequence
have no zeros on the disk boundary is necessary. For example, consider the unit disk, and the sequence
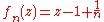
for all It converges uniformly to
It converges uniformly to 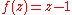 which has no zeros inside of this disk, but each
which has no zeros inside of this disk, but each 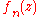 has exactly one zero in the disk, which is
has exactly one zero in the disk, which is 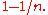
This result holds more generally for any bounded
convex set
s but it is most useful to state for disks.
An immediate consequence of this theorem is the following corollary
. If is an open set and a sequence of holomorphic functions
is an open set and a sequence of holomorphic functions 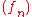 converges uniformly on compact subsets of
converges uniformly on compact subsets of  to a holomorphic function
to a holomorphic function 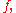 and furthermore if
and furthermore if  is not zero at any point in
is not zero at any point in  , then
, then  is either identically zero or also is never zero.
is either identically zero or also is never zero.
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a field within mathematics, Hurwitz's theorem, named after Adolf Hurwitz
Adolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
, roughly states that, under certain conditions, if a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s converges uniformly to a holomorphic function on compact sets, then after a while those functions and the limit function have the same number of zeros
Zero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
in any open disk.
More precisely, let
 be an open set
be an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, and consider a sequence of holomorphic functions
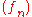 which converges uniformly on compact subsets of
which converges uniformly on compact subsets of  to a holomorphic function
to a holomorphic function 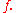 Let
Let  be an open disk of center
be an open disk of center  and radius
and radius  which is contained in
which is contained in  together with its boundary
together with its boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
. Assume that
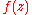 has no zeros on the disk boundary. Then, there exists a natural number
has no zeros on the disk boundary. Then, there exists a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
 such that for all
such that for all  greater than
greater than  the functions
the functions 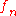 and
and  have the same number of zeros in
have the same number of zeros in 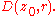
The requirement that
 have no zeros on the disk boundary is necessary. For example, consider the unit disk, and the sequence
have no zeros on the disk boundary is necessary. For example, consider the unit disk, and the sequence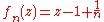
for all
 It converges uniformly to
It converges uniformly to 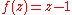 which has no zeros inside of this disk, but each
which has no zeros inside of this disk, but each 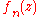 has exactly one zero in the disk, which is
has exactly one zero in the disk, which is 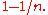
This result holds more generally for any bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
s but it is most useful to state for disks.
An immediate consequence of this theorem is the following corollary
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
. If
 is an open set and a sequence of holomorphic functions
is an open set and a sequence of holomorphic functions 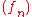 converges uniformly on compact subsets of
converges uniformly on compact subsets of  to a holomorphic function
to a holomorphic function 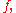 and furthermore if
and furthermore if  is not zero at any point in
is not zero at any point in  , then
, then  is either identically zero or also is never zero.
is either identically zero or also is never zero.

