
Homology manifold
Encyclopedia
In mathematics
, a homology manifold (or generalized manifold)
is a locally compact topological space X that looks locally like a topological manifold
from the point of view of homology theory
.
such that for any x∈X, the homology groups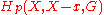
are trivial unless p=n, in which case they are isomorphic to G. Here H is some homology theory, usually singular homology. Homology manifolds are the same as homology Z-manifolds.
More generally, one can define homology manifolds with boundary, by allowing the local homology groups to vanish
at some points, which are of course called the boundary of the homology manifold. The boundary of an n-dimensional first-countable homology manifold is an n−1 dimensional homology manifold (without boundary).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a homology manifold (or generalized manifold)
is a locally compact topological space X that looks locally like a topological manifold
Topological manifold
In mathematics, a topological manifold is a topological space which looks locally like Euclidean space in a sense defined below...
from the point of view of homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
.
Definition
A homology G-manifold (without boundary) of dimension n over an abelian group G of coefficients is a locally compact topological space X with finite G-cohomological dimensionCohomological dimension
In abstract algebra, cohomological dimension is an invariant which measures the homological complexity of representations of a group. It has important applications in geometric group theory, topology, and algebraic number theory....
such that for any x∈X, the homology groups
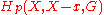
are trivial unless p=n, in which case they are isomorphic to G. Here H is some homology theory, usually singular homology. Homology manifolds are the same as homology Z-manifolds.
More generally, one can define homology manifolds with boundary, by allowing the local homology groups to vanish
at some points, which are of course called the boundary of the homology manifold. The boundary of an n-dimensional first-countable homology manifold is an n−1 dimensional homology manifold (without boundary).
Examples
- Any topological manifold is a homology manifold.
- An example of a homology manifold that is not a manifold is the suspension of a homology sphereHomology sphereIn algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
that is not a sphere. - If X×Y is a topological manifolds, then X and Y are homology manifolds.

