
Homogeneously Suslin set
Encyclopedia
In descriptive set theory
, a set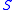 is said to be homogeneously Suslin if it is the projection of a homogeneous tree.
is said to be homogeneously Suslin if it is the projection of a homogeneous tree. 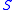 is said to be
is said to be  -homogeneously Suslin if it is the projection of a
-homogeneously Suslin if it is the projection of a  -homogeneous tree.
-homogeneous tree.
If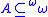 is a
is a 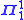 set and
set and  is a measurable cardinal, then
is a measurable cardinal, then  is
is  -homogeneously Suslin. This result is important in the proof that the existence of a measurable cardinal
-homogeneously Suslin. This result is important in the proof that the existence of a measurable cardinal
implies that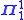 sets are determined
sets are determined
.
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
, a set
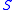 is said to be homogeneously Suslin if it is the projection of a homogeneous tree.
is said to be homogeneously Suslin if it is the projection of a homogeneous tree. 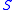 is said to be
is said to be  -homogeneously Suslin if it is the projection of a
-homogeneously Suslin if it is the projection of a  -homogeneous tree.
-homogeneous tree.If
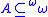 is a
is a 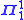 set and
set and  is a measurable cardinal, then
is a measurable cardinal, then  is
is  -homogeneously Suslin. This result is important in the proof that the existence of a measurable cardinal
-homogeneously Suslin. This result is important in the proof that the existence of a measurable cardinalMeasurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
implies that
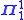 sets are determined
sets are determinedDeterminacy
In set theory, a branch of mathematics, determinacy is the study of under what circumstances one or the other player of a game must have a winning strategy, and the consequences of the existence of such strategies.-Games:...
.

