Hirschman uncertainty
Encyclopedia
In quantum mechanics
, information theory
, and Fourier analysis, the Hirschman uncertainty is defined as the sum of the temporal and spectral Shannon entropies. It turns out that Heisenberg's uncertainty principle
can be expressed as a lower bound on the sum of these entropies. This is stronger than the usual statement of the uncertainty principle in terms of the product of standard deviations.
In 1957, Hirschman considered a function f and its Fourier transform
g such that
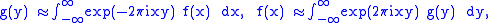
where the "
" indicates convergence in 
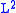, and normalized so that (by Plancherel's theorem
)
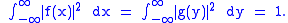
He showed that for any such functions the sum of the Shannon entropies is non-negative:
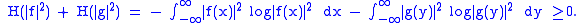
A tighter bound,
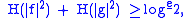
was conjectured by Hirschman and Everett
and proven in 1975 by W. Beckner.. The equality holds in the case of Gaussian distributions,
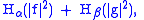where 
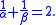For simplicity we shall consider this inequality only in one dimension; the extension to multiple dimensions is not difficult and can be found in the literature cited.
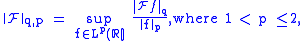and 
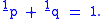
In 1961, Babenko found this norm for even integer values of q. Finally, in 1975,
using Hermite functions as eigenfunctions of the Fourier transform, Beckner proved that the value of this norm (in one dimension) for all
is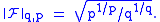
Thus we have the Babenko–Beckner inequality
that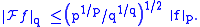
can be derived.
Letting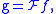
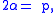and 
so that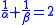 
and 
we have
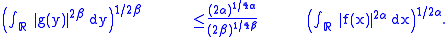
Squaring both sides and taking the logarithm, we get:
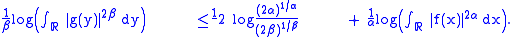
Multiplying both sides by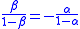
reverses the sense of the inequality: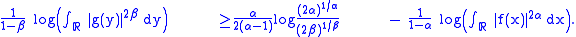
Rearranging terms, we finally get an inequality in terms of the sum of the Rényi entropies:
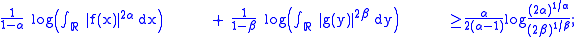
Note that this inequality is symmetric with respect to
and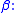 
We no longer have to assume that 
only that they are positive and not both one, and that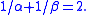 
To see this symmetry, simply exchange the rôles of 
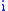and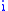 
in the Fourier transform.
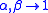yields the Shannon entropy inequality
valid for any base of logarithm as long as we choose an appropriate unit of information, bit
, nat
, etc. The constant will be different, though, for a different normalization of the Fourier transform, (such as is usually used in physics,) i.e.
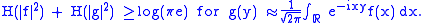
In this case the dilation of the Fourier transform by a factor of
simply adds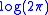 
to its entropy.
and entropy
: it is a problem of the calculus of variations
to show that this distribution maximizes entropy for a given variance, and at the same time minimizes the variance for a given entropy. Moreover the Fourier transform of a Gaussian probability amplitude function is also Gaussian—and the absolute squares of both of these are Gaussian, too. This suggests—and it is in fact quite true—that the entropic statement of the uncertainty principle is stronger than its traditional statement in terms of the variance or standard deviation.
Hirschman explained that entropy—his version of entropy was the negative of Shannon's—is a "measure of the concentration of [a probability distribution] in a set of small measure." Thus a low or large negative Shannon entropy means that a considerable mass of the probability distribution is confined to a set of small measure. Note that this set of small measure need not be contiguous; a probability distribution can have several concentrations of mass in intervals of small measure, and the entropy may still be low no matter how widely scattered those intervals are.
This is not the case with the variance: variance measures the concentration of mass about the mean of the distribution, and a low variance means that a considerable mass of the probability distribution is concentrated in a contiguous interval of small measure.
To make this distinction more formal, we say that two probability density functions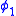
and 
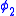are equimeasurable if:
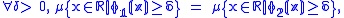
where
is the Lebesgue measure
. Any two equimeasurable probability density functions have the same Shannon entropy, and in fact the same Rényi entropy of any order. The same is not true of variance, however. Any probability density function has a radially decreasing equimeasurable "rearrangement" whose variance is less (up to translation) than any other rearrangement of the function; and there exist rearrangements of arbitrarily high variance, (all having the same entropy.)
In fact, for any probability density function
on the real line,
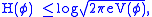
where H is the Shannon entropy and V is the variance, an inequality that is saturated only in the case of a normal distribution.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, and Fourier analysis, the Hirschman uncertainty is defined as the sum of the temporal and spectral Shannon entropies. It turns out that Heisenberg's uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
can be expressed as a lower bound on the sum of these entropies. This is stronger than the usual statement of the uncertainty principle in terms of the product of standard deviations.
In 1957, Hirschman considered a function f and its Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
g such that
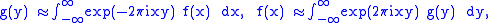
where the "
" indicates convergence in 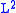, and normalized so that (by Plancherel's theoremPlancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
)
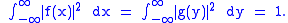
He showed that for any such functions the sum of the Shannon entropies is non-negative:
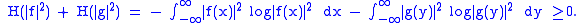
A tighter bound,
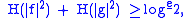
was conjectured by Hirschman and Everett
Hugh Everett
Hugh Everett III was an American physicist who first proposed the many-worlds interpretation of quantum physics, which he termed his "relative state" formulation....
and proven in 1975 by W. Beckner.. The equality holds in the case of Gaussian distributions,
Sketch of proof
The proof of this tight inequality depends on the so-called (q, p)-norm of the Fourier transformation. (Establishing this norm is the most difficult part of the proof.) From this norm we are able to establish a lower bound on the sum of the (differential) Rényi entropiesRényi entropy
In information theory, the Rényi entropy, a generalisation of Shannon entropy, is one of a family of functionals for quantifying the diversity, uncertainty or randomness of a system...
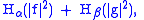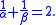where For simplicity we shall consider this inequality only in one dimension; the extension to multiple dimensions is not difficult and can be found in the literature cited.Babenko–Beckner inequality
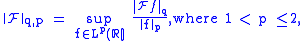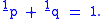
The (q, p)-norm of the Fourier transform is defined to be and In 1961, Babenko found this norm for even integer values of q. Finally, in 1975,
using Hermite functions as eigenfunctions of the Fourier transform, Beckner proved that the value of this norm (in one dimension) for all
is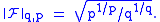Thus we have the Babenko–Beckner inequality
Babenko–Beckner inequality
In mathematics, the Babenko–Beckner inequality is a sharpened form of the Hausdorff–Young inequality having applications to uncertainty principles in the Fourier analysis of Lp spaces...
that
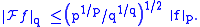
Rényi entropy inequality
From this inequality, an expression of the uncertainty principal in terms of the Rényi entropyRényi entropy
In information theory, the Rényi entropy, a generalisation of Shannon entropy, is one of a family of functionals for quantifying the diversity, uncertainty or randomness of a system...
can be derived.
Letting
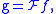
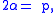and so that 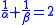and we have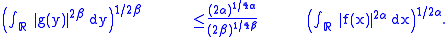Squaring both sides and taking the logarithm, we get:
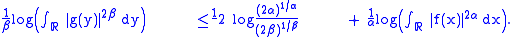
Multiplying both sides by
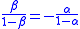reverses the sense of the inequality: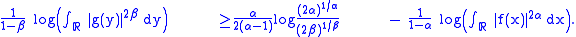Rearranging terms, we finally get an inequality in terms of the sum of the Rényi entropies:
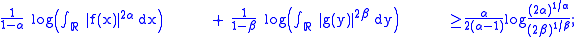
Note that this inequality is symmetric with respect to
and 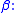We no longer have to assume that only that they are positive and not both one, and that 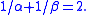To see this symmetry, simply exchange the rôles of 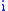and 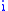in the Fourier transform.Shannon entropy inequality
Taking the limit of this last inequality as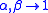 yields the Shannon entropy inequalityvalid for any base of logarithm as long as we choose an appropriate unit of information, bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
, nat
Nat (information)
A nat is a logarithmic unit of information or entropy, based on natural logarithms and powers of e, rather than the powers of 2 and base 2 logarithms which define the bit. The nat is the natural unit for information entropy...
, etc. The constant will be different, though, for a different normalization of the Fourier transform, (such as is usually used in physics,) i.e.
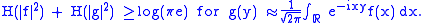
In this case the dilation of the Fourier transform by a factor of
simply adds 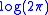to its entropy.Entropy versus variance
The Gaussian or normal probability distribution plays an important role in the relationship between varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
and entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
: it is a problem of the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
to show that this distribution maximizes entropy for a given variance, and at the same time minimizes the variance for a given entropy. Moreover the Fourier transform of a Gaussian probability amplitude function is also Gaussian—and the absolute squares of both of these are Gaussian, too. This suggests—and it is in fact quite true—that the entropic statement of the uncertainty principle is stronger than its traditional statement in terms of the variance or standard deviation.
Hirschman explained that entropy—his version of entropy was the negative of Shannon's—is a "measure of the concentration of [a probability distribution] in a set of small measure." Thus a low or large negative Shannon entropy means that a considerable mass of the probability distribution is confined to a set of small measure. Note that this set of small measure need not be contiguous; a probability distribution can have several concentrations of mass in intervals of small measure, and the entropy may still be low no matter how widely scattered those intervals are.
This is not the case with the variance: variance measures the concentration of mass about the mean of the distribution, and a low variance means that a considerable mass of the probability distribution is concentrated in a contiguous interval of small measure.
To make this distinction more formal, we say that two probability density functions
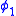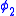and are equimeasurable if: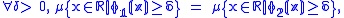where
is the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. Any two equimeasurable probability density functions have the same Shannon entropy, and in fact the same Rényi entropy of any order. The same is not true of variance, however. Any probability density function has a radially decreasing equimeasurable "rearrangement" whose variance is less (up to translation) than any other rearrangement of the function; and there exist rearrangements of arbitrarily high variance, (all having the same entropy.)
In fact, for any probability density function
on the real line,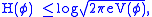where H is the Shannon entropy and V is the variance, an inequality that is saturated only in the case of a normal distribution.
See also
- Inequalities in information theoryInequalities in information theoryInequalities are very important in the study of information theory. There are a number of different contexts in which these inequalities appear.-Shannon-type inequalities:...
- Uncertainty principleUncertainty principleIn quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
- Riesz-Thorin theoremRiesz-Thorin theoremIn mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.This theorem bounds the norms of linear maps...
Further reading
- S. Zozor, C. Vignat. On classes of non-Gaussian asymptotic minimizers in entropic uncertainty principles. arXiv:math/0605510v1