Hierarchical hidden Markov model
Encyclopedia
The hierarchical hidden Markov model (HHMM) is a statistical model
derived from the hidden Markov model
(HMM). In an HHMM each state is considered to be a self-contained probabilistic model. More precisely each state of the HHMM is itself an HHMM.
HHMM's and HMM's are useful in many fields, including pattern recognition
. They are kinds of Markov process
es
facilitate learning and generalization. For example, even though a fully connected HMM could always be used if enough training data is available it is often useful to constrain the model by not allowing arbitrary state transitions. In the same way it can be beneficial to embed the HMM into a greater structure; which, theoretically, may not be able to solve any other problems than the basic HMM but can solve some problems more efficiently when it comes to the amount of training data required.
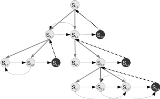
When a state in an HHMM is activated, it will activate its own probabilistic model, i.e. it will activate one of the states of the underlying HHMM, which in turn may activate its underlying HHMM and so on. The process is repeated until a special state, called a production state, is activated. Only the production states emit observation symbols in the usual HMM sense. When the production state has emitted a symbol, control returns to the state that activated the production state.
The states that do not directly emit observations symbols are called internal states. The activation of a state in an HHMM under an internal state is called a vertical transition. After a vertical transition is completed a horizontal transition occurs to a state within the same level. When a horizontal transition leads to a terminating state control is returned to
the state in the HHMM, higher up in the hierarchy, that produced the last vertical transition.
Remember that a vertical transition can result in more vertical transitions before reaching a sequence of production states and
finally returning to the top level. Thus the production states visited gives rise to a sequence of observation symbols that is "produced" by the state at the top level.
The methods for estimating the HHMM parameters and model structure are more complex than for the HMM and the interested reader is referred to (Fine et al., 1998).
It should be pointed out that the HMM and HHMM belong to the same class of classifiers. That is, they can be used to solve the
same set of problems. In fact, the HHMM can be transformed into a standard HMM. However, the HHMM utilizes its structure to solve a subset of the problems more efficiently.
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
derived from the hidden Markov model
Hidden Markov model
A hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
(HMM). In an HHMM each state is considered to be a self-contained probabilistic model. More precisely each state of the HHMM is itself an HHMM.
HHMM's and HMM's are useful in many fields, including pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
. They are kinds of Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
es
Background
It is sometimes useful to use HMMs in specific structures in order tofacilitate learning and generalization. For example, even though a fully connected HMM could always be used if enough training data is available it is often useful to constrain the model by not allowing arbitrary state transitions. In the same way it can be beneficial to embed the HMM into a greater structure; which, theoretically, may not be able to solve any other problems than the basic HMM but can solve some problems more efficiently when it comes to the amount of training data required.
The hierarchical hidden Markov model
In the hierarchical hidden Markov model (HHMM) each state is considered to be a self-contained probabilistic model. More precisely each state of the HHMM is itself an HHMM. This implies that the states of the HHMM emit sequences of observation symbols rather than single observation symbols as is the case for the standard HMM states.The states that do not directly emit observations symbols are called internal states. The activation of a state in an HHMM under an internal state is called a vertical transition. After a vertical transition is completed a horizontal transition occurs to a state within the same level. When a horizontal transition leads to a terminating state control is returned to
the state in the HHMM, higher up in the hierarchy, that produced the last vertical transition.
Remember that a vertical transition can result in more vertical transitions before reaching a sequence of production states and
finally returning to the top level. Thus the production states visited gives rise to a sequence of observation symbols that is "produced" by the state at the top level.
The methods for estimating the HHMM parameters and model structure are more complex than for the HMM and the interested reader is referred to (Fine et al., 1998).
It should be pointed out that the HMM and HHMM belong to the same class of classifiers. That is, they can be used to solve the
same set of problems. In fact, the HHMM can be transformed into a standard HMM. However, the HHMM utilizes its structure to solve a subset of the problems more efficiently.