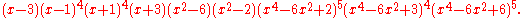In the mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 field of graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, the Harries graph or Harries (3-10)-cage is a 3-regular

Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...

 undirected graph with 70 vertices and 105 edges.

The Harries graph has chromatic number 2, chromatic index 3, radius 6, diameter 6, girth 10 and is Hamiltonian. It is also a 3-vertex-connected

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

 and 3-edge-connected

K-edge-connected graph

In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G =  be an arbitrary graph....

 non-planar

Planar graph

In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

 cubic graph

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....

.

The characteristic polynomial

Characteristic polynomial

In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

 of the Harries graph is

History

In 1972, A. T. Balaban published a (3-10)-cage graph, a cubic graph that has as few vertices as possible for girth 10. It was the first (3-10)-cage discovered but it was not unique.

The complete list of (3-10)-cage and the proof of minimality was given by O'Keefe and Wong in 1980. There exist three distinct (3-10)-cage graphs—the Balaban 10-cage

Balaban 10-cage

In the mathematical field of graph theory, the Balaban 10-cage or Balaban -cage is a 3-regular graph with 70 vertices and 105 edges named after A. T. Balaban. Published in 1972, It was the first -cage discovered but is not unique....

, the Harries graph and the Harries–Wong graph

Harries–Wong graph

In the mathematical field of graph theory, the Harries–Wong graph is a 3-regular undirected graph with 70 vertices and 105 edges.The Harries–Wong graph has chromatic number 2, chromatic index 3, radius 6, diameter 6, girth 10 and is Hamiltonian...

. Moreover, the Harries–Wong graph graph and Harries graph are cospectral graphs

Spectral graph theory

In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....

.