
Hardy–Littlewood zeta-function conjectures
Encyclopedia
In mathematics, the Hardy–Littlewood zeta-function conjectures, named after Godfrey Harold Hardy and John Edensor Littlewood
, are two conjectures concerning the distances between zeros and the density of zeros of the Riemann zeta function.
In 1914 Godfrey Harold Hardy
proved that the Riemann zeta function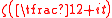 has infinitely many real zeros.
has infinitely many real zeros.
Let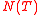 be the total number of real zeros,
be the total number of real zeros, 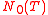 be the total number of zeros of odd order of the function
be the total number of zeros of odd order of the function 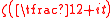 , lying on the interval
, lying on the interval
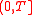 .
.
Hardy and Littlewood claimed two conjectures. These conjectures – on the distance between real zeros of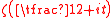 and on the density of zeros of
and on the density of zeros of 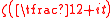 on intervals
on intervals  for sufficiently great
for sufficiently great  ,
, 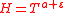 and with as less as possible value of
and with as less as possible value of  , where
, where  is an arbitrarily small number – open two new directions in the investigation of the Riemann zeta function.
is an arbitrarily small number – open two new directions in the investigation of the Riemann zeta function.
1. For any there exists such
there exists such 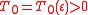 that for
that for  and
and 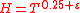 the interval
the interval  contains a zero of odd order of the function
contains a zero of odd order of the function 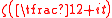 .
.
2. For any there exist
there exist 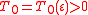 and
and  , such that for
, such that for  and
and 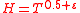 the inequality
the inequality 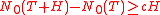 is true.
is true.
In 1942 Atle Selberg
studied the problem 2 and proved that for any there exists such
there exists such 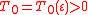 and
and  , such that for
, such that for  and
and 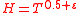 the inequality
the inequality 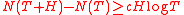 is true.
is true.
In his turn, Selberg
claim his conjecture that it's possible to decrease the value of the exponent for
for 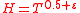 which was proved forty-two years later by A.A. Karatsuba.
which was proved forty-two years later by A.A. Karatsuba.
John Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
, are two conjectures concerning the distances between zeros and the density of zeros of the Riemann zeta function.
In 1914 Godfrey Harold Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
proved that the Riemann zeta function
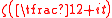 has infinitely many real zeros.
has infinitely many real zeros.Let
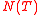 be the total number of real zeros,
be the total number of real zeros, 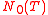 be the total number of zeros of odd order of the function
be the total number of zeros of odd order of the function 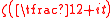 , lying on the interval
, lying on the interval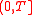 .
.Hardy and Littlewood claimed two conjectures. These conjectures – on the distance between real zeros of
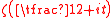 and on the density of zeros of
and on the density of zeros of 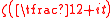 on intervals
on intervals  for sufficiently great
for sufficiently great  ,
, 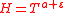 and with as less as possible value of
and with as less as possible value of  , where
, where  is an arbitrarily small number – open two new directions in the investigation of the Riemann zeta function.
is an arbitrarily small number – open two new directions in the investigation of the Riemann zeta function.1. For any
 there exists such
there exists such 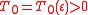 that for
that for  and
and 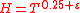 the interval
the interval  contains a zero of odd order of the function
contains a zero of odd order of the function 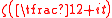 .
.2. For any
 there exist
there exist 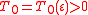 and
and  , such that for
, such that for  and
and 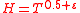 the inequality
the inequality 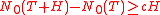 is true.
is true.In 1942 Atle Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
studied the problem 2 and proved that for any
 there exists such
there exists such 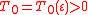 and
and  , such that for
, such that for  and
and 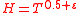 the inequality
the inequality 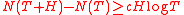 is true.
is true.In his turn, Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
claim his conjecture that it's possible to decrease the value of the exponent
 for
for 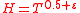 which was proved forty-two years later by A.A. Karatsuba.
which was proved forty-two years later by A.A. Karatsuba.

