
Hardy–Littlewood tauberian theorem
Encyclopedia
In mathematical analysis
, the Hardy–Littlewood tauberian theorem is a tauberian theorem relating the asymptotics of the partial sums of a series
with the asymptotics of its Abel summation. In this form, the theorem asserts that if, as y ↓ 0,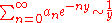
then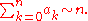
The integral
formulation of the theorem relates in an analogous manner the asymptotics of the cumulative distribution function
of a function with the asymptotics of its Laplace transform.
The theorem was proved in 1914 by G. H. Hardy
and J. E. Littlewood. In 1930 Jovan Karamata
gave a new and much simpler proof.
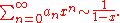
Then as n goes to ∞ we have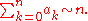
The theorem is sometimes quoted in equivalent forms, where instead of requiring an ≥ 0, we require an = O(1), or we require an ≥ −K for some constant K. The theorem is sometimes quoted in another equivalent formulation (through the change of variable x = 1/ey ). If, as y ↓ 0,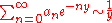
then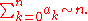
. The Laplace–Stieltjes transform of F is defined by the Stieltjes integral
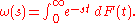
The theorem relates the asymptotics of ω with those of F in the following way. If ρ is a non-negative real number, then the following are equivalent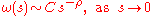
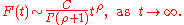
Here Γ denotes the Gamma function
. One obtains the theorem for series as a special case by taking ρ = 1 and F(t) to be a piecewise constant function with value between t=n and t=n+1.
between t=n and t=n+1.
A slight improvement is possible. A function L(x) is slowly varying at infinity if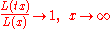
for every positive t. Let L be a function slowly varying at infinity and ρ a non-negative real number. Then the following are equivalent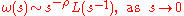
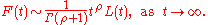
proved an extension of Tauber
's converse of Abel's theorem
. Littlewood showed the following: If an = O(1/n ), and as x ↑ 1 we have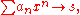
then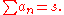
This came historically before the Hardy–Littlewood tauberian theorem, but can be proved as an simple application of it.
based on their tauberian theorem; they proved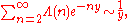
where Λ is the von Mangoldt function
, and then conclude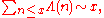
an equivalent form of the prime number theorem.
Littlewood developed a simpler proof, still based on this tauberian theorem, in 1971.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, the Hardy–Littlewood tauberian theorem is a tauberian theorem relating the asymptotics of the partial sums of a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
with the asymptotics of its Abel summation. In this form, the theorem asserts that if, as y ↓ 0,
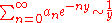
then
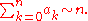
The integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
formulation of the theorem relates in an analogous manner the asymptotics of the cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
of a function with the asymptotics of its Laplace transform.
The theorem was proved in 1914 by G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
and J. E. Littlewood. In 1930 Jovan Karamata
Jovan Karamata
Jovan Karamata was one of the greatest Serbian mathematicians of the 20th century. He is remembered for contributions to analysis, in particular, the Tauberian theory and the theory of slowly varying functions...
gave a new and much simpler proof.
Series formulation
This formulation is from Titchmarsh. Suppose an ≥ 0 for all n, and as x ↑ 1 we have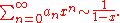
Then as n goes to ∞ we have
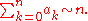
The theorem is sometimes quoted in equivalent forms, where instead of requiring an ≥ 0, we require an = O(1), or we require an ≥ −K for some constant K. The theorem is sometimes quoted in another equivalent formulation (through the change of variable x = 1/ey ). If, as y ↓ 0,
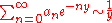
then
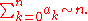
Integral formulation
The following more general formulation is from Feller. Consider a real-valued function F : [0,∞) → R of bounded variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
. The Laplace–Stieltjes transform of F is defined by the Stieltjes integral
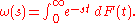
The theorem relates the asymptotics of ω with those of F in the following way. If ρ is a non-negative real number, then the following are equivalent
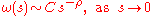
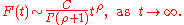
Here Γ denotes the Gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. One obtains the theorem for series as a special case by taking ρ = 1 and F(t) to be a piecewise constant function with value
 between t=n and t=n+1.
between t=n and t=n+1.A slight improvement is possible. A function L(x) is slowly varying at infinity if
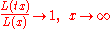
for every positive t. Let L be a function slowly varying at infinity and ρ a non-negative real number. Then the following are equivalent
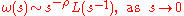
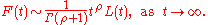
Littlewood's extension of Tauber's theorem
In 1911 LittlewoodJohn Edensor Littlewood
John Edensor Littlewood was a British mathematician, best known for the results achieved in collaboration with G. H. Hardy.-Life:...
proved an extension of Tauber
Alfred Tauber
Alfred Tauber was a mathematician who was born in Bratislava, and died in the Theresienstadt concentration camp. In 1897 he proved a corrected converse of Abel's theorem. G.H. Hardy and J.E. Littlewood coined the term Tauberian to describe converse theorems like that proved by Tauber.- External...
's converse of Abel's theorem
Abel's theorem
In mathematics, Abel's theorem for power series relates a limit of a power series to the sum of its coefficients. It is named after Norwegian mathematician Niels Henrik Abel.-Theorem:...
. Littlewood showed the following: If an = O(1/n ), and as x ↑ 1 we have
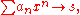
then
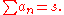
This came historically before the Hardy–Littlewood tauberian theorem, but can be proved as an simple application of it.
Prime number theorem
In 1915 Hardy and Littlewood developed a proof of the prime number theoremPrime number theorem
In number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
based on their tauberian theorem; they proved
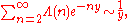
where Λ is the von Mangoldt function
Von Mangoldt function
In mathematics, the von Mangoldt function is an arithmetic function named after German mathematician Hans von Mangoldt.-Definition:The von Mangoldt function, conventionally written as Λ, is defined as...
, and then conclude
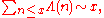
an equivalent form of the prime number theorem.
Littlewood developed a simpler proof, still based on this tauberian theorem, in 1971.

