
Gyrokinetics
Encyclopedia
Gyrokinetics is a branch of plasma physics derived from kinetics
and electromagnetism
used to describe the low-frequency phenomena in a plasma. The trajectory of charged particles in a magnetic field is a helix that winds around the field line. This trajectory can be decomposed into a relatively slow motion of the guiding center
along the field line and a fast circular motion called cyclotronic motion. For most of the plasma physics problems, this later motion is irrelevant. Gyrokinetics yields a way of describing the evolution of the particles without taking into account the circular motion, thus discarding the useless information of the cyclotronic angle.
that yields the evolution of the distribution function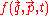 of one particle species in a non collisional plasma,
of one particle species in a non collisional plasma,

where is the Hamiltonian of a single particle, and the brackets are Poisson brackets.
is the Hamiltonian of a single particle, and the brackets are Poisson brackets.
We denote the unit vector along the magnetic field as .
.
The first step is to perform a variable change, from canonical phase-space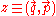 to guiding center coordinates
to guiding center coordinates 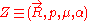 , where
, where 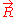 is the position of the guiding center,
is the position of the guiding center,  is the parallel velocity,
is the parallel velocity,  is the magnetic moment, and
is the magnetic moment, and  is the cyclotronic angle.
is the cyclotronic angle.
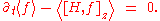
 where the new magnetic moment is an exact invariant, and the Vlasov equation take a simple form,
where the new magnetic moment is an exact invariant, and the Vlasov equation take a simple form,
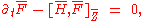
where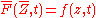 , and
, and  is the gyrokinetic Hamiltonian.
is the gyrokinetic Hamiltonian.
Kinetics (physics)
In physics and engineering, kinetics is a term for the branch of classical mechanics that is concerned with the relationship between the motion of bodies and its causes, namely forces and torques...
and electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
used to describe the low-frequency phenomena in a plasma. The trajectory of charged particles in a magnetic field is a helix that winds around the field line. This trajectory can be decomposed into a relatively slow motion of the guiding center
Guiding center
In many cases of practical interest, the motion in a magnetic field of an electrically charged particle can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point...
along the field line and a fast circular motion called cyclotronic motion. For most of the plasma physics problems, this later motion is irrelevant. Gyrokinetics yields a way of describing the evolution of the particles without taking into account the circular motion, thus discarding the useless information of the cyclotronic angle.
Derivation of the gyrokinetics equations
The starting point is the Vlasov equationVlasov equation
The Vlasov equation is a differential equation describing time evolution of the distribution function of plasma consisting of charged particles with long-range interaction...
that yields the evolution of the distribution function
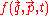 of one particle species in a non collisional plasma,
of one particle species in a non collisional plasma,
where
 is the Hamiltonian of a single particle, and the brackets are Poisson brackets.
is the Hamiltonian of a single particle, and the brackets are Poisson brackets.We denote the unit vector along the magnetic field as
 .
.The first step is to perform a variable change, from canonical phase-space
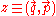 to guiding center coordinates
to guiding center coordinates 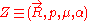 , where
, where 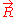 is the position of the guiding center,
is the position of the guiding center,  is the parallel velocity,
is the parallel velocity,  is the magnetic moment, and
is the magnetic moment, and  is the cyclotronic angle.
is the cyclotronic angle.Classical perturbation theory
A first way to derive the gyrokinetics equations is to take the average of the Vlasov equation over the cyclotronic angle,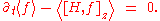
Modern gyrokinetics
A more modern way to derive the gyrokinetics equations is to use the Lie transformation theory to change the coordinates to a system where the new magnetic moment is an exact invariant, and the Vlasov equation take a simple form,
where the new magnetic moment is an exact invariant, and the Vlasov equation take a simple form,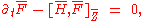
where
 , and
, and  is the gyrokinetic Hamiltonian.
is the gyrokinetic Hamiltonian.

