Grüneisen Parameter
Encyclopedia
The Grüneisen parameter, γ, named after Eduard Grüneisen
, describes the effect that changing the volume of a crystal lattice has on its vibrational properties
, and, as a consequence, the effect that changing temperature has on the size or dynamics of the lattice. The term is usually reserved to describe the single thermodynamic property γ, which is a weighted average of the many separate parameters γi entering the original Grüneisen's formulation in terms of the phonon
nonlinearities.
), there are many formulations of the Grüneisen parameter which are equally valid, leading to numerous distinct yet correct interpretations of its meaning.
Some formulations for the Grüneisen parameter include:
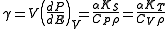
where V is volume,
and 
are the principal (i.e. per-mass) heat capacities at constant pressure and volume, E is energy, α is the volume thermal expansion coefficient
,
and 
are the adiabatic and isothermal bulk moduli, and ρ is density.
model for the vibrating atoms within a crystal.
When the restoring force acting on an atom displaced from its equilibrium position is linear
in the atom's displacement, the frequencies ωi of individual phonon
s do not depend on the volume of the crystal or on the presence of other phonons, and the thermal expansion (and thus γ) is zero. When the restoring force is non-linear in the displacement, the phonon frequencies ωi change with the volume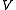
. The Grüneisen parameter of an individual vibrational mode 
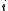can then be defined as (the negative of) the logarithmic derivative of the corresponding frequency 
:
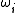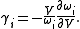
For example,
one can show that
if one defines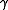
as the weighted average
where
's are the partial vibrational mode contributions to the heat capacity, such that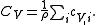 
and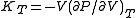
,
by noting that
and thus
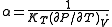
To calculate the partial derivative in this equation, let us first relate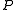
to the internal energy 
. Writing the thermodynamic relationship
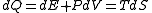
as
,
we conclude that
,
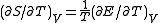and
.
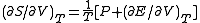Using
,
we find the relationship between
and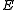 
:
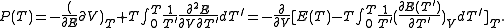
The derivative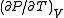
can then be calculated, resulting in
We can now express the latter partial derivatine via the parameters of the quasi-harmonic model.
The internal energy is related to the vibrational mode frequencies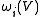
via
where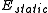
is the equilibrium energy of the lattice, and 
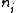is the statistical occupation of the 
's mode, given by the Bose-Einstein distribution,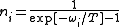 
. Since the only value that depends on the volume are the frequencies 
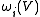, the heat capacity per unit volume is
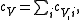where
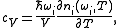
and the principal heat capacity is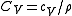
.
The expression for
then reduces to
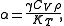
where by definition
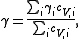
yielding the required relationship.
Gruneisen parameter has no units
Eduard Grüneisen
Eduard Grüneisen was a German physicist; co-eponym of Mie-Grüneisen equation of state.Grüneisen was born in Giebichenstein.The Grüneisen Parameter was named after him....
, describes the effect that changing the volume of a crystal lattice has on its vibrational properties
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
, and, as a consequence, the effect that changing temperature has on the size or dynamics of the lattice. The term is usually reserved to describe the single thermodynamic property γ, which is a weighted average of the many separate parameters γi entering the original Grüneisen's formulation in terms of the phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
nonlinearities.
Thermodynamic definitions
Because of the equivalences between many properties and derivatives within thermodynamics (e.g. see Maxwell RelationsMaxwell relations
Maxwell's relations are a set of equations in thermodynamics which are derivable from the definitions of the thermodynamic potentials. The Maxwell relations are statements of equality among the second derivatives of the thermodynamic potentials. They follow directly from the fact that the order of...
), there are many formulations of the Grüneisen parameter which are equally valid, leading to numerous distinct yet correct interpretations of its meaning.
Some formulations for the Grüneisen parameter include:
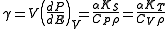
where V is volume,
and are the principal (i.e. per-mass) heat capacities at constant pressure and volume, E is energy, α is the volume thermal expansion coefficientThermal expansion
Thermal expansion is the tendency of matter to change in volume in response to a change in temperature.When a substance is heated, its particles begin moving more and thus usually maintain a greater average separation. Materials which contract with increasing temperature are rare; this effect is...
,
and are the adiabatic and isothermal bulk moduli, and ρ is density.Microscopic definition via the phonon frequencies
The physical meaning of the parameter can also be extended by combining thermodynamics with a reasonable microphysicsMicrophysics
The term microphysics refers to areas of physics that study phenomena that take place on the microscopic scale , such as:* Quantum mechanics* Molecular physics* Atomic physics* Nuclear physics* Particle physics...
model for the vibrating atoms within a crystal.
When the restoring force acting on an atom displaced from its equilibrium position is linear
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
in the atom's displacement, the frequencies ωi of individual phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s do not depend on the volume of the crystal or on the presence of other phonons, and the thermal expansion (and thus γ) is zero. When the restoring force is non-linear in the displacement, the phonon frequencies ωi change with the volume
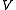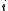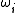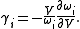
. The Grüneisen parameter of an individual vibrational mode can then be defined as (the negative of) the logarithmic derivative of the corresponding frequency :Relationship between microscopic and thermodynamic models
Using the quasi-harmonic approximation for atomic vibrations, the macroscopic Grüneisen parameter (γ) can be related to the description of how the vibration frequencies (phonons) within a crystal are altered with changing volume (i.e. γi's).For example,
one can show that
if one defines
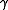as the weighted averagewhere
's are the partial vibrational mode contributions to the heat capacity, such that 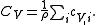Derivation
To arrive at this result, one can start from the definitions of the two key quantities,and
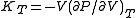,by noting that
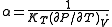
and thusTo calculate the partial derivative in this equation, let us first relate
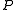to the internal energy . Writing the thermodynamic relationship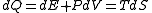as
,we conclude that
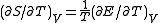,and
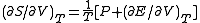.Using
,we find the relationship between
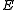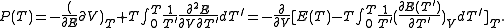
and :The derivative
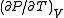can then be calculated, resulting inWe can now express the latter partial derivatine via the parameters of the quasi-harmonic model.
The internal energy is related to the vibrational mode frequencies
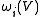viawhere
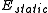is the equilibrium energy of the lattice, and 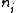is the statistical occupation of the 's mode, given by the Bose-Einstein distribution, 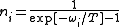. Since the only value that depends on the volume are the frequencies 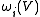, the heat capacity per unit volume is 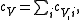where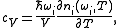and the principal heat capacity is
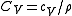.The expression for
then reduces to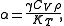where by definition
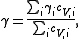
yielding the required relationship.
External links
Gruneisen parameter has no units