Grover's algorithm
Encyclopedia
Grover's algorithm is a quantum algorithm
for searching an unsorted
database
with N entries in O(N1/2) time and using O(log N) storage space (see big O notation
). It was invented by Lov Grover in 1996.
In models of classical computation, searching an unsorted database cannot be done in less than linear time (so merely searching through every item
is optimal). Grover's algorithm illustrates that in the quantum model searching can be done faster than this; in fact its time complexity O(N1/2) is asymptotically the fastest possible for searching an unsorted database in the quantum model. It provides a quadratic speedup, unlike other quantum algorithms, which may provide exponential speedup over their classical counterparts. However, even quadratic speedup is considerable when N is large.
Like many quantum algorithms, Grover's algorithm is probabilistic in the sense that it gives the correct answer with high probability
. The probability of failure can be decreased by repeating the algorithm. (An example of a deterministic quantum algorithm is the Deutsch-Jozsa algorithm
, which always produces the correct answer.)
Grover's algorithm can also be used for estimating the mean
and median
of a set of numbers, and for solving the Collision problem. The algorithm can be further optimized if there is more than one matching entry and the number of matches is known beforehand.
H, which can be supplied by n=log2 N qubit
s. Consider the problem of determining the index of the database entry which satisfies some search criterion. Let f be the function which maps database entries to 0 or 1, where f(ω)=1 and ω satisfies the search criterion. We are provided with (quantum black box) access to a subroutine
in the form of a unitary operator
, Uω, which acts as: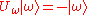
Our goal is to identify the index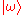
.
denote the uniform superposition over all states
.
Then the operator
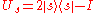
is known as the Grover diffusion operator.
Here is the algorithm:
,
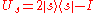is that Uω can be expressed in an alternate way:
.
To prove this it suffices to check how Uω acts on basis states:
.
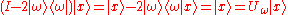for all 
.
The following computations show what happens in the first iteration: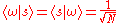
.
.
.
.
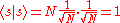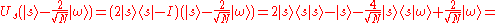
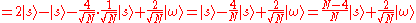After application of the two operators (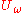
and 
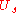), the amplitude of the searched-for element has increased from 
to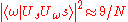 
.
In geometric terms, the angle θ between |ω⟩ and |s⟩ is given by:
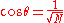
The operator Uω is a reflection at the hyperplane orthogonal to |ω⟩; for vectors in the plane spanned by |s⟩ and |ω⟩, it acts as a reflection at the line through |ω×⟩. The operator Us is a reflection at the line through |s⟩. Therefore, the state vector remains in the plane spanned by |s⟩ and |ω⟩ after each application of Us and after each application of Uω, and it is straightforward to check that the operator UsUω of each Grover iteration step rotates the state vector by an angle of
.
We need to stop when the state vector passes close to |ω⟩; after this, subsequent iterations rotate the state vector away from |ω⟩, reducing the probability of obtaining the correct answer. The exact probability of measuring the correct answer is: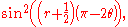
where r is the (integer) number of Grover iterations.
The earliest time that we get a near-optimal measurement is therefore
.
. A natural way to do this is by eigenvalue analysis of a matrix. Notice that during the entire computation, the state of the algorithm is a linear combination of 
and 
. We can write the action of 
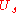and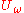 
in the space spanned by 
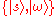as: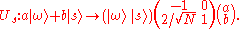
So in the basis
(which is neither orthogonal nor a basis of the whole space) the action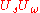 
of applying 
followed by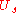 
is given by the matrix
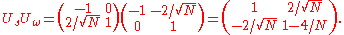
This matrix happens to have a very convenient Jordan form. If we define
, it is
where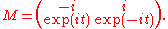 
It follows that rth power of the matrix (corresponding to r iterations) is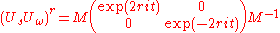
Using this form we can use trigonometric identities to compute the probability of observing ω after r iterations mentioned in the previous section,
.
Alternatively, one might reasonably imagine that a near-optimal time to distinguish would be when the angles 2rt and -2rt are as far apart as possible, which corresponds to
or 
. Then the system is in state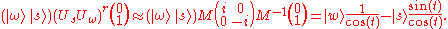
A short calculation now shows that the observation yields the correct answer ω with error O(1/N).
There are several ways to handle the case if k is unknown. For example, one could run Grover's algorithm several times, with
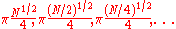
iterations. For any k, one of iterations will find a matching entry with a sufficiently high probability. The total number of iterations is at most
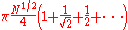
which is still O(N1/2).
It can be shown that this could be improved. If the number of marked items is k, where k is unknown, there is an algorithm that finds the solution in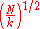
queries. This fact is used in order to solve the collision problem.
If the Grover's search problem was solvable with logc N applications of Uω, that would imply that NP is contained in BQP
, by transforming problems in NP into Grover-type search problems. The optimality of
Grover's algorithm suggests (but does not prove) that NP is not contained in BQP.
The number of iterations for k matching entries, π(N/k)1/2/4, is also optimal.
Quantum algorithm
In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a...
for searching an unsorted
Sorting
Sorting is any process of arranging items in some sequence and/or in different sets, and accordingly, it has two common, yet distinct meanings:# ordering: arranging items of the same kind, class, nature, etc...
database
Database
A database is an organized collection of data for one or more purposes, usually in digital form. The data are typically organized to model relevant aspects of reality , in a way that supports processes requiring this information...
with N entries in O(N1/2) time and using O(log N) storage space (see big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
). It was invented by Lov Grover in 1996.
In models of classical computation, searching an unsorted database cannot be done in less than linear time (so merely searching through every item
Linear search
In computer science, linear search or sequential search is a method for finding a particular value in a list, that consists of checking every one of its elements, one at a time and in sequence, until the desired one is found....
is optimal). Grover's algorithm illustrates that in the quantum model searching can be done faster than this; in fact its time complexity O(N1/2) is asymptotically the fastest possible for searching an unsorted database in the quantum model. It provides a quadratic speedup, unlike other quantum algorithms, which may provide exponential speedup over their classical counterparts. However, even quadratic speedup is considerable when N is large.
Like many quantum algorithms, Grover's algorithm is probabilistic in the sense that it gives the correct answer with high probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
. The probability of failure can be decreased by repeating the algorithm. (An example of a deterministic quantum algorithm is the Deutsch-Jozsa algorithm
Deutsch-Jozsa algorithm
The Deutsch–Jozsa algorithm is a quantum algorithm, proposed by David Deutsch and Richard Jozsa in 1992 with improvements by Richard Cleve, Artur Ekert, Chiara Macchiavello, and Michele Mosca in 1998...
, which always produces the correct answer.)
Applications
Although the purpose of Grover's algorithm is usually described as "searching a database", it may be more accurate to describe it as "inverting a function". Roughly speaking, if we have a function y=f(x) that can be evaluated on a quantum computer, this algorithm allows us to calculate x when given y. Inverting a function is related to the searching of a database because we could come up with a function that produces a particular value of y if x matches a desired entry in a database, and another value of y for other values of x.Grover's algorithm can also be used for estimating the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of a set of numbers, and for solving the Collision problem. The algorithm can be further optimized if there is more than one matching entry and the number of matches is known beforehand.
Setup
Consider an unsorted database with N entries. The algorithm requires an N-dimensional state spaceMathematical formulation of quantum mechanics
The mathematical formulations of quantum mechanics are those mathematical formalisms that permit a rigorous description of quantum mechanics. Such are distinguished from mathematical formalisms for theories developed prior to the early 1900s by the use of abstract mathematical structures, such as...
H, which can be supplied by n=log2 N qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s. Consider the problem of determining the index of the database entry which satisfies some search criterion. Let f be the function which maps database entries to 0 or 1, where f(ω)=1 and ω satisfies the search criterion. We are provided with (quantum black box) access to a subroutine
Subroutine
In computer science, a subroutine is a portion of code within a larger program that performs a specific task and is relatively independent of the remaining code....
in the form of a unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
, Uω, which acts as:
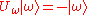
Our goal is to identify the index
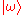.Algorithm steps
The steps of Grover's algorithm are given as follows. Let denote the uniform superposition over all states.Then the operator
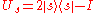
is known as the Grover diffusion operator.
Here is the algorithm:
- Initialize the system to the state
-
- Perform the following "Grover iteration" r(N) times. The function r(N), which is asymptotically O(N½), is described below.
- Apply the operator
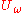. - Apply the operator
.
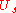- Apply the operator
- Perform the measurement Ω. The measurement result will be λω with probability approaching 1 for N≫1. From λω, ω may be obtained.
The first iteration
A preliminary observation, in parallel with our definition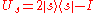,is that Uω can be expressed in an alternate way:
.To prove this it suffices to check how Uω acts on basis states:
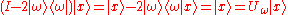. for all .The following computations show what happens in the first iteration:
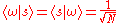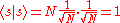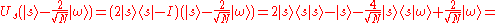
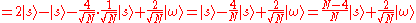....After application of the two operators (
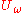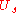and ), the amplitude of the searched-for element has increased from to 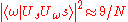.Geometric proof of correctness
Consider the plane spanned by |s⟩ and |ω⟩. Let |ω×⟩ be a ket in this plane perpendicular to |ω⟩. Since |ω⟩ is one of the basis vectors, the overlap isIn geometric terms, the angle θ between |ω⟩ and |s⟩ is given by:
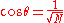
The operator Uω is a reflection at the hyperplane orthogonal to |ω⟩; for vectors in the plane spanned by |s⟩ and |ω⟩, it acts as a reflection at the line through |ω×⟩. The operator Us is a reflection at the line through |s⟩. Therefore, the state vector remains in the plane spanned by |s⟩ and |ω⟩ after each application of Us and after each application of Uω, and it is straightforward to check that the operator UsUω of each Grover iteration step rotates the state vector by an angle of
.We need to stop when the state vector passes close to |ω⟩; after this, subsequent iterations rotate the state vector away from |ω⟩, reducing the probability of obtaining the correct answer. The exact probability of measuring the correct answer is:
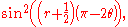
where r is the (integer) number of Grover iterations.
The earliest time that we get a near-optimal measurement is therefore
.Algebraic proof of correctness
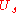To complete the algebraic analysis we need to find out what happens when we repeatedly apply. A natural way to do this is by eigenvalue analysis of a matrix. Notice that during the entire computation, the state of the algorithm is a linear combination of and . We can write the action of and 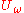in the space spanned by 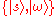as: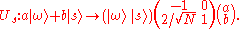So in the basis
(which is neither orthogonal nor a basis of the whole space) the action 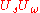of applying followed by 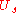is given by the matrix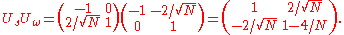This matrix happens to have a very convenient Jordan form. If we define
, it is where 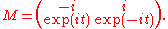It follows that rth power of the matrix (corresponding to r iterations) is
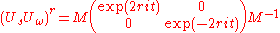
Using this form we can use trigonometric identities to compute the probability of observing ω after r iterations mentioned in the previous section,
.Alternatively, one might reasonably imagine that a near-optimal time to distinguish would be when the angles 2rt and -2rt are as far apart as possible, which corresponds to
or . Then the system is in state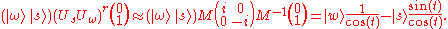A short calculation now shows that the observation yields the correct answer ω with error O(1/N).
Extensions
If, instead of 1 matching entry, there are k matching entries, the same algorithm works but the number of iterations must be π(N/k)1/2/4 instead of πN1/2/4.There are several ways to handle the case if k is unknown. For example, one could run Grover's algorithm several times, with
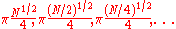
iterations. For any k, one of iterations will find a matching entry with a sufficiently high probability. The total number of iterations is at most
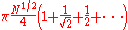
which is still O(N1/2).
It can be shown that this could be improved. If the number of marked items is k, where k is unknown, there is an algorithm that finds the solution in
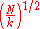queries. This fact is used in order to solve the collision problem.Optimality
It is known that Grover's algorithm is optimal. That is, any algorithm that accesses the database only by using the operator Uω must apply Uω at least as many times as Grover's algorithm. This result is important in understanding the limits of quantum computation.If the Grover's search problem was solvable with logc N applications of Uω, that would imply that NP is contained in BQP
BQP
In computational complexity theory BQP is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances...
, by transforming problems in NP into Grover-type search problems. The optimality of
Grover's algorithm suggests (but does not prove) that NP is not contained in BQP.
The number of iterations for k matching entries, π(N/k)1/2/4, is also optimal.