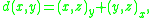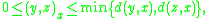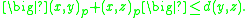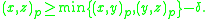In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Gromov product is a concept in the theory of metric space

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

s named after the mathematician Mikhail Gromov. Intuitively, the Gromov product measures the distance for which two geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s starting at the same point remain "close together". The Gromov product can also be used to define δ-hyperbolic metric spaces in the sense of Gromov.

Definition

Let (X, d) be a metric space and let x, y, z ∈ X. Then the Gromov product of y and z at x, denoted (y, z)_x, is defined by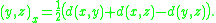

Properties

• The Gromov product is symmetric: (y, z)_x = (z, y)_x.

• The Gromov product degenerates at the endpoints: (y, z)_y = (y, z)_z = 0.

• For any points p, q, x, y and z,

• As mentioned in the introduction, the Gromov product measures how long geodesics remain close together. Namely, if x, y and z are three points of a δ-hyperbolic metric space then the initial segments of length (y, z)_x of geodesics from x to y and x to z are no further than 2δ apart (in the sense of the Hausdorff distance
  Hausdorff distance
  In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right...
  
  between closed sets).

• In fact, the Gromov product can be used to define δ-hyperbolic spaces in the sense of Gromov: (X, d) is said to be δ-hyperbolic if, for all p, x, y and z in X,