In queueing theory

Queueing theory

Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...

, a discipline within the mathematical theory of probability

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

, the Gordon–Newell theorem is an extension of Jackson's theorem from open queueing networks to closed queueing networks of exponential servers. We cannot apply Jackson's theorem to closed networks because the queue length at a node in the closed network is limited by the population of the network. The Gordon–Newell theorem calculates the open network solution and then eliminates the infeasible states by renormalizing the probabilities. Calculation of the normalizing constant

Normalizing constant

The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...

 makes the treatment more awkward as the whole state space must be enumerated. Buzen's algorithm

Buzen's algorithm

In queueing theory, a discipline within the mathematical theory of probability, Buzen's algorithm is an algorithm for calculating the normalization constant G in the Gordon–Newell theorem. This method was first proposed by Jeffrey P. Buzen in 1973. Once G is computed the probability distributions...

 or mean value analysis

Mean value analysis

In queueing theory, a specialty within the mathematical theory of probability, mean value analysis is a technique for computing expected queue lengths in equilibrium for a closed separable system of queues...

 can be used to calculate the normalizing constant more efficiently.

Definition of a Gordon–Newell network

A network of m interconnected queues is known as a Gordon–Newell network or closed Jackson network if it meets the following conditions:

1. the network is closed (no customers can enter or leave the network),
2. all service times are exponentially distributed and the service discipline at all queues is FCFS,
3. a customer completing service at queue i will move to queue j with probability 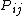, with the 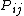such that ,
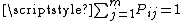4. the utilization
   Utilization
   Utilization is a statistical concept as well as a primary business measure for the rental industry.-Queueing theory:In queueing theory, utilization is the proportion of the system's resources which is used by the traffic which arrives at it. It should be strictly less than one for the system to...
   
   of all of the queues is less than one.

Theorem

In a closed Gordon–Newell network of m queues, with a total population of K individuals, write (where k_i is the length of queue i) for the state of the network and S(K, m) for the state space


Then the equilibrium state probability distribution exists and is given by


where service times at queue i are exponentially distributed with parameter μ_i. The normalizing constant G(K) is given by


and e_i is the visit ratio, calculated by solving the simultaneous equations