
Mean value analysis
Encyclopedia
In queueing theory
, a specialty within the mathematical theory of probability, mean value analysis is a technique for computing expected
queue lengths in equilibrium for a closed separable system of queues. It was developed by Reiser and Lavenberg in 1980.
It is based on the arrival theorem, which states that when one customer in an M-customer closed system arrives at a service facility he/she observes the rest of the system to be in the equilibrium state for a system with M − 1 customers.
Let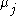 be the (known) service rate for queue j, i.e.
be the (known) service rate for queue j, i.e. 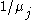 is the service time.
is the service time.
Let P be the (known) routing matrix, where each element pij is the probability that after visiting queue i the customer will visit queue j. From this matrix we can calculate the vector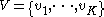 known as the visit-ratio vector by solving the eigenvector-like equation
known as the visit-ratio vector by solving the eigenvector-like equation 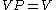 .
.
Let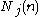 be the mean number of customers in queue j when there are a total of n customers in the system; this includes the job currently being served in queue j.
be the mean number of customers in queue j when there are a total of n customers in the system; this includes the job currently being served in queue j.
Let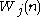 be the mean time spent by a customer in queue j when there are a total of n in the system; it is the total delay at this queue including the customer service time.
be the mean time spent by a customer in queue j when there are a total of n in the system; it is the total delay at this queue including the customer service time.
Initialization. Let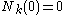 for k = 1 to K
for k = 1 to K
Repeat for m = 1 to M:
End repeat.
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, a specialty within the mathematical theory of probability, mean value analysis is a technique for computing expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
queue lengths in equilibrium for a closed separable system of queues. It was developed by Reiser and Lavenberg in 1980.
It is based on the arrival theorem, which states that when one customer in an M-customer closed system arrives at a service facility he/she observes the rest of the system to be in the equilibrium state for a system with M − 1 customers.
Problem setup
Consider a closed queueing network of K queues, with M customers circulating in the system.Let
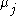 be the (known) service rate for queue j, i.e.
be the (known) service rate for queue j, i.e. 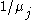 is the service time.
is the service time.Let P be the (known) routing matrix, where each element pij is the probability that after visiting queue i the customer will visit queue j. From this matrix we can calculate the vector
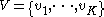 known as the visit-ratio vector by solving the eigenvector-like equation
known as the visit-ratio vector by solving the eigenvector-like equation 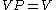 .
.Let
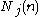 be the mean number of customers in queue j when there are a total of n customers in the system; this includes the job currently being served in queue j.
be the mean number of customers in queue j when there are a total of n customers in the system; this includes the job currently being served in queue j.Let
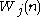 be the mean time spent by a customer in queue j when there are a total of n in the system; it is the total delay at this queue including the customer service time.
be the mean time spent by a customer in queue j when there are a total of n in the system; it is the total delay at this queue including the customer service time.Algorithm
The algorithm starts with an empty network (zero customers), then increases the number of customers by 1 until it reaches the desired number of customers M.Initialization. Let
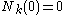 for k = 1 to K
for k = 1 to KRepeat for m = 1 to M:
- Step 1. For k = 1 to K let
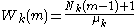 . (This is based on the arrival theorem).
. (This is based on the arrival theorem).
- Step 2. Let
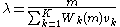 . (This is an application of Little's LawLittle's lawIn the mathematical theory of queues, Little's result, theorem, lemma, law or formula says:It is a restatement of the Erlang formula, based on the work of Danish mathematician Agner Krarup Erlang...
. (This is an application of Little's LawLittle's lawIn the mathematical theory of queues, Little's result, theorem, lemma, law or formula says:It is a restatement of the Erlang formula, based on the work of Danish mathematician Agner Krarup Erlang...
to find the system throughput).
- Step 3. Let
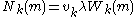 for k = 1 to K. (This is another application of Little's law to each individual queue).
for k = 1 to K. (This is another application of Little's law to each individual queue).
End repeat.
External links
- J. Virtamo: Queuing networks. Handout from Helsinki Tech gives good overview of Jackson's Theorem and MVA.
- Simon Lam: A simple derivation of the MVA algorithm. Shows relationship between Buzen's algorithmBuzen's algorithmIn queueing theory, a discipline within the mathematical theory of probability, Buzen's algorithm is an algorithm for calculating the normalization constant G in the Gordon–Newell theorem. This method was first proposed by Jeffrey P. Buzen in 1973. Once G is computed the probability distributions...
and MVA.

