Godunov's scheme
Encyclopedia
In numerical analysis
and computational fluid dynamics
, Godunov's scheme is a conservative
numerical scheme
, suggested by S. K. Godunov
in 1959, for solving partial differential equations. In this method, the conservative variables are considered as piecewise constant over the mesh cells at each time step and the time evolution is determined by the exact solution of the Riemann problem
(shock tube) at the inter-cell boundaries (Hirsch, 1990).
Following Hirsch, the scheme involves three distinct steps to obtain the solution at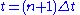
from the known solution at 
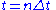, as follows:
Step 1 Define piecewise constant approximation of the solution at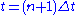
. Since the piecewise constant approximation is an average of the solution over the cell of size 
, the spatial error is of order 
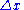, and hence the resulting scheme will be first-order accurate in space.
Note that this approximation corresponds to a finite volume method
representation whereby the discrete values represent averages of the state variables over the cells. Exact relations for the averaged cell values can be obtained from the integral conservation laws.
Step 2 Obtain the solution for the local Riemann problem at the cell interfaces. This is the only physical step of the whole procedure. The discontinuities at the interfaces are resolved in a superposition of waves satisfying locally the conservation equations.
The original Godunov method is based upon the exact solution of the Riemann problems. However, approximate solutions can be applied as an alternative.
Step 3 Average the state variables after a time interval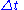
. The state variables obtained after Step 2 are averaged over each cell defining a new piecewise constant approximation resulting from the wave propagation during the time interval 
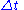. To be consistent, the time interval 
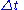should be limited such that the waves emanating from an interface do not interact with waves created at the adjacent interfaces. Otherwise the situation inside a cell would be influenced by interacting Riemann problems. This leads to the CFL
condition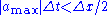
where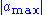 
is the maximum wave speed obtained from the cell eigenvalue(s) of the local Jacobian matrix.
The first and third steps are solely of a numerical nature and can be considered as a projection stage, independent of the second, physical step, the evolution stage. Therefore, they can be modified without influencing the physical input, for instance by replacing the piecewise constant approximation by a piecewise linear variation inside each cell, leading to the definition of second-order space-accurate schemes, such as the MUSCL scheme
.
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
and computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
, Godunov's scheme is a conservative
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
numerical scheme
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, suggested by S. K. Godunov
Sergei K. Godunov
Sergei Konstantinovich Godunov is professor at the Sobolev Institute of Mathematics of the Russian Academy of Sciences in Novosibirsk, Russia....
in 1959, for solving partial differential equations. In this method, the conservative variables are considered as piecewise constant over the mesh cells at each time step and the time evolution is determined by the exact solution of the Riemann problem
Riemann problem
A Riemann problem, named after Bernhard Riemann, consists of a conservation law together with piecewise constant data having a single discontinuity. The Riemann problem...
(shock tube) at the inter-cell boundaries (Hirsch, 1990).
Following Hirsch, the scheme involves three distinct steps to obtain the solution at
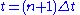from the known solution at 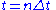, as follows:Step 1 Define piecewise constant approximation of the solution at
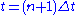. Since the piecewise constant approximation is an average of the solution over the cell of size , the spatial error is of order 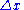, and hence the resulting scheme will be first-order accurate in space.Note that this approximation corresponds to a finite volume method
Finite volume method
The finite volume method is a method for representing and evaluating partial differential equations in the form of algebraic equations [LeVeque, 2002; Toro, 1999]....
representation whereby the discrete values represent averages of the state variables over the cells. Exact relations for the averaged cell values can be obtained from the integral conservation laws.
Step 2 Obtain the solution for the local Riemann problem at the cell interfaces. This is the only physical step of the whole procedure. The discontinuities at the interfaces are resolved in a superposition of waves satisfying locally the conservation equations.
The original Godunov method is based upon the exact solution of the Riemann problems. However, approximate solutions can be applied as an alternative.
Step 3 Average the state variables after a time interval
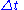. The state variables obtained after Step 2 are averaged over each cell defining a new piecewise constant approximation resulting from the wave propagation during the time interval 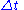. To be consistent, the time interval 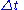should be limited such that the waves emanating from an interface do not interact with waves created at the adjacent interfaces. Otherwise the situation inside a cell would be influenced by interacting Riemann problems. This leads to the CFLCourant–Friedrichs–Lewy condition
In mathematics, the Courant–Friedrichs–Lewy condition is a necessary condition for convergence while solving certain partial differential equations numerically by the method of finite differences. It arises when explicit time-marching schemes are used for the numerical solution...
condition
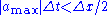where 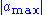is the maximum wave speed obtained from the cell eigenvalue(s) of the local Jacobian matrix.The first and third steps are solely of a numerical nature and can be considered as a projection stage, independent of the second, physical step, the evolution stage. Therefore, they can be modified without influencing the physical input, for instance by replacing the piecewise constant approximation by a piecewise linear variation inside each cell, leading to the definition of second-order space-accurate schemes, such as the MUSCL scheme
MUSCL scheme
In the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
.
See also
- Godunov's theoremGodunov's theoremIn numerical analysis and computational fluid dynamics, Godunov's theorem — also known as Godunov's order barrier theorem — is a mathematical theorem important in the development of the theory of high resolution schemes for the numerical solution of partial differential equations.The theorem states...
- High-resolution scheme
- MUSCL schemeMUSCL schemeIn the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
- Sergei K. GodunovSergei K. GodunovSergei Konstantinovich Godunov is professor at the Sobolev Institute of Mathematics of the Russian Academy of Sciences in Novosibirsk, Russia....
- Total variation diminishingTotal variation diminishingIn numerical methods, total variation diminishing is a property of certain discretization schemes used to solve hyperbolic partial differential equations...
- Lax–Wendroff theorem
Further reading
- Laney, Culbert B. (1998), Computational Gas Dynamics, Cambridge University Press.
- Toro, E. F. (1999), Riemann Solvers and Numerical Methods for Fluid Dynamics, Springer-Verlag.
- Tannehill, John C., et al., (1997), Computational Fluid mechanics and Heat Transfer, 2nd Ed., Taylor and Francis.
- Wesseling, Pieter (2001), Principles of Computational Fluid Dynamics, Springer-Verlag.