Ginzburg criterion
Encyclopedia
Mean field theory
gives sensible results as long as we are able to neglect fluctuations in the system under consideration. The Ginzburg Criterion tells us quantitatively when mean field theory is valid. It also gives the idea of an upper critical dimension, a dimensionality of the system above which mean field theory gives proper results, and the critical exponents predicted by mean field theory match exactly with those obtained by numerical methods.
Example: Ising Model
If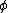 
is the order parameter of the system, then mean field theory requires that the fluctuations in the order parameter are much smaller than the actual value of the order parameter near the critical point.
Quantitatively, this means that
Using this in the Landau theory
, which is identical to the mean field theory for the Ising model, the value of the upper critical dimension comes out to be 4. If the dimension of the space is greater than 4, the mean-field results are good and self-consistent. But for dimensions less than 4, the predictions are less accurate. For instance, in one dimension, the mean field approximation predicts a phase transition for the Ising model, whereas we know that there is none from the exact analytic solution that can be evaluated in one dimension.
Mean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
gives sensible results as long as we are able to neglect fluctuations in the system under consideration. The Ginzburg Criterion tells us quantitatively when mean field theory is valid. It also gives the idea of an upper critical dimension, a dimensionality of the system above which mean field theory gives proper results, and the critical exponents predicted by mean field theory match exactly with those obtained by numerical methods.
Example: Ising ModelIsing modelThe Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
If 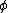is the order parameter of the system, then mean field theory requires that the fluctuations in the order parameter are much smaller than the actual value of the order parameter near the critical point.Quantitatively, this means that
Using this in the Landau theory
Landau theory
Landau theory in physics was introduced by Lev Landau in an attempt to formulate a general theory of second-order phase transitions. He was motivated to suggest that the free energy of any system should obey two conditions: that the free energy is analytic, and that it obeys the symmetry of the...
, which is identical to the mean field theory for the Ising model, the value of the upper critical dimension comes out to be 4. If the dimension of the space is greater than 4, the mean-field results are good and self-consistent. But for dimensions less than 4, the predictions are less accurate. For instance, in one dimension, the mean field approximation predicts a phase transition for the Ising model, whereas we know that there is none from the exact analytic solution that can be evaluated in one dimension.