Generalized semi-infinite programming
Encyclopedia
In mathematics
, a semi-infinite programming (SIP) problem is an optimization problem with a finite number of variables and an infinite number of constraints. The constraints are typically parameterized. In a generalized semi-infinite programming (GSIP) problem, the feasible set of the parameters depends on the variables.
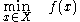
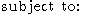
where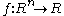
In the special case that the set :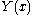
is nonempty for all 
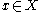GSIP can be cast as bilevel programs (Multilevel programming
).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a semi-infinite programming (SIP) problem is an optimization problem with a finite number of variables and an infinite number of constraints. The constraints are typically parameterized. In a generalized semi-infinite programming (GSIP) problem, the feasible set of the parameters depends on the variables.
Mathematical formulation of the problem
The problem can be stated simply as: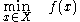
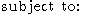
where
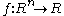
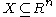
In the special case that the set :
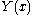is nonempty for all 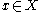GSIP can be cast as bilevel programs (Multilevel programmingMultilevel programming
The "level" refers to sets of variables. A bilevel program has two sets:min f: x in X, y in Y, h=0, g=0.A reason for identifying levels is to apply a decomposition principle for algorithm design. One example is the bilinear program...
).
See also
- optimizationOptimization (mathematics)In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
- Semi-Infinite Programming (SIP)