Generalized scale-free model
Encyclopedia
There has been a burst of activity in the modeling of scale-free complex networks. The recipe of Barabási and Albert has been followed by several variations and generalizations and the revamping of previous mathematical
works. As long as there is a power law
distribution in a model, it is a scale-free network
, and a model of that network is a scale-free model.
1. Adding or removing nodes
. Usually we concentrate on growing the network, i.e. adding nodes.
2. Preferential attachment
: The probability
that new nodes will be connected to the "old" node.
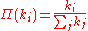
and adds one new node at every time step.
(Note, another general feature of
in real
networks is that
, i.e. there is a nonzero probability that a
new node attaches to an isolated node. Thus in general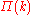
has the form
,
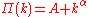where
is the initial attractiveness of the node.)
nodes linked to it but also on the number of links in each of these nodes.
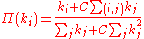, where C is a coefficient between 0 and 1.
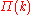that a node attaches to node 
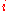is proportional to the degree
of node 
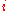. This assumption involves two hypotheses: first, that 
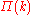depends on 
, in contrast to random graphs in which 
, and second, that the functional form of 
is linear in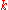 
. The precise form of 
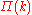is not necessary linear, and recent studies have demonstrated that the degree distribution depends strongly on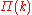 
Krapivsky, Redner, and Leyvraz demonstrate that the scale-free nature of the network is destroyed for nonlinear preferential attachment. The only case in which the topology of the network is scale free is that in which the preferential attachment is asymptotically
linear, i.e.
as 
. In this case the rate equation leads to
This way the exponent of the degree distribution can be tuned to any value between 2 and
.
The iterative construction leading to a hierarchical network. Starting from a fully connected cluster of five nodes, we create four identical replicas connecting the peripheral nodes of each cluster to the central node of the original cluster. From this, we get a network of 25 nodes (N = 25).
Repeating the same process, we can create four more replicas of the original cluster - the four peripheral nodes of each one connect to the central node of the nodes created in the first step. This gives N = 125, and the process can continue indefinitely.
works. As long as there is a power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
distribution in a model, it is a scale-free network
Scale-free network
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P of nodes in the network having k connections to other nodes goes for large values of k as...
, and a model of that network is a scale-free model.
Features
Many real networks are scale-free networks, which require scale-free models to describe them. There are two ingredients needed to build up a scale-free model:1. Adding or removing nodes
Node (networking)
In communication networks, a node is a connection point, either a redistribution point or a communication endpoint . The definition of a node depends on the network and protocol layer referred to...
. Usually we concentrate on growing the network, i.e. adding nodes.
2. Preferential attachment
Preferential attachment
A preferential attachment process is any of a class of processes in which some quantity, typically some form of wealth or credit, is distributed among a number of individuals or objects according to how much they already have, so that those who are already wealthy receive more than those who are not...
: The probability
that new nodes will be connected to the "old" node.Examples
There have been several attempts to generate scale-free network properties. Here are some examples:The Barabási–Albert model
For example, the first scale-free model, the Barabási–Albert model, has a linear preferential attachment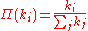and adds one new node at every time step.
(Note, another general feature of
in realnetworks is that
, i.e. there is a nonzero probability that anew node attaches to an isolated node. Thus in general
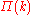has the form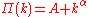,where
is the initial attractiveness of the node.)Two-level network model
Dangalchev builds a 2-L model by adding a second-order preferential attachment. The attractiveness of a node in the 2-L model depends not only on the number ofnodes linked to it but also on the number of links in each of these nodes.
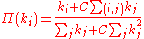, where C is a coefficient between 0 and 1.Non-linear preferential attachment
The Barabási–Albert model assumes that the probability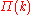that a node attaches to node 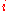is proportional to the degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
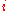of node . This assumption involves two hypotheses: first, that 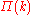depends on , in contrast to random graphs in which , and second, that the functional form of is linear in 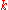. The precise form of 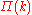is not necessary linear, and recent studies have demonstrated that the degree distribution depends strongly on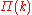 Krapivsky, Redner, and Leyvraz demonstrate that the scale-free nature of the network is destroyed for nonlinear preferential attachment. The only case in which the topology of the network is scale free is that in which the preferential attachment is asymptotically
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
linear, i.e.
as . In this case the rate equation leads to
This way the exponent of the degree distribution can be tuned to any value between 2 and
.Hierarchical network model
There is another kind of scale-free model, which grows according to some patterns, such as the hierarchical network model.The iterative construction leading to a hierarchical network. Starting from a fully connected cluster of five nodes, we create four identical replicas connecting the peripheral nodes of each cluster to the central node of the original cluster. From this, we get a network of 25 nodes (N = 25).
Repeating the same process, we can create four more replicas of the original cluster - the four peripheral nodes of each one connect to the central node of the nodes created in the first step. This gives N = 125, and the process can continue indefinitely.