Generalized forces
Encyclopedia
Generalized forces are defined via coordinate transformation of applied forces, 
, on a system
of n particles, i. The concept finds use in Lagrangian mechanics
, where it plays a conjugate role to generalized coordinates
.
A convenient equation from which to derive the expression for generalized forces is that of the virtual work
,
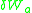, caused by applied forces, as seen in D'Alembert's principle
in accelerating systems and the principle of virtual work for applied forces in static systems. The subscript
is used here to indicate that this virtual work only accounts for the applied forces, a distinction which is important in dynamic systems.
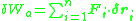
Substitute the definition for the virtual displacement (differential):
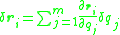
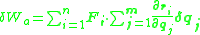
Using the distributive property of multiplication over addition and the associative property of addition, we have
.
By analogy with the way work is defined in classical mechanics, we define the generalized force as:
.
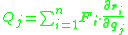Thus, the virtual work due to the applied forces is
.
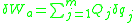, on a systemPhysical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
of n particles, i. The concept finds use in Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, where it plays a conjugate role to generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
.
A convenient equation from which to derive the expression for generalized forces is that of the virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
,
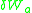, caused by applied forces, as seen in D'Alembert's principleD'Alembert's principle
D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert...
in accelerating systems and the principle of virtual work for applied forces in static systems. The subscript
is used here to indicate that this virtual work only accounts for the applied forces, a distinction which is important in dynamic systems.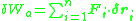
-
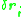is the virtual displacement of the system, which does not have to be consistent with the constraints (in this development)
Substitute the definition for the virtual displacement (differential):
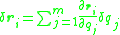
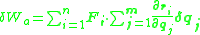
Using the distributive property of multiplication over addition and the associative property of addition, we have
.By analogy with the way work is defined in classical mechanics, we define the generalized force as:
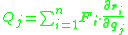.Thus, the virtual work due to the applied forces is
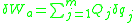.See also
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- Generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
- Degrees of freedom (physics and chemistry)Degrees of freedom (physics and chemistry)A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
- Virtual workVirtual workVirtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...