Generalized additive model for location, scale and shape
Encyclopedia
In statistics
, the generalized additive model location, scale and shape (GAMLSS) is a class of statistical model
that provides extended capabilities compared to the simpler generalized linear model
s and generalized additive model
s. These simpler models allow the typical values of a quantity being modelled to be related to whatever explanatory variables are available. Here the "typical value" is more formally a location parameter
, which only describes a limited aspect of the probability distribution
of the dependent variable. The GAMLSS approach allows other parameters
of the distribution to be related to the explanatory variables; where these other parameters might be interpreted as scale
and shape parameter
s of the distribution, although the approach is not limited to such parameters.
s (GLMs) and generalized additive model
s (GAMs).
In GAMLSS the exponential family
distribution
assumption for the response variable, (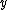
), (essential in GLMs
and GAMs
), is relaxed and replaced by a general distribution family, including highly skew
and/or kurtotic
continuous and discrete distributions.
The systematic part of the model is expanded to allow modeling not only of the mean
(or location
) but other parameters of the distribution of y as linear and/or nonlinear, parametric and/or additive non-parametric functions of explanatory variables and/or random effects.
GAMLSS is especially suited for modelling leptokurtic or platykurtic and/or positive or negative skew response variable. For count type response variable data it deals with over-dispersion by using proper over-dispersed discrete distributions. Heterogeneity also is dealt with by modelling the scale
or shape parameter
s using explanatory variables. There are several packages written in R
related to GAMLSS models.).
A GAMLSS model assumes independent observations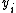
for 
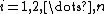
with probability (density) function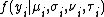
conditional on 
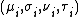a vector of four distribution parameters, each of which can be a function to the explanatory variables. The first two population distribution parameters 
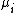and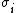 
are usually characterized as location and scale parameters, while the remaining parameter(s), if any, are characterized as shape parameters, e.g. skewness
and kurtosis
parameters, although the model may be applied more generally to the parameters of any population distribution with up to four distribution parameters, and can be generalized to more than four distribution parameters.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the generalized additive model location, scale and shape (GAMLSS) is a class of statistical model
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
that provides extended capabilities compared to the simpler generalized linear model
Generalized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
s and generalized additive model
Generalized additive model
In statistics, the generalized additive model is a statistical model developed by Trevor Hastie and Rob Tibshirani for blending properties of generalized linear models with additive models....
s. These simpler models allow the typical values of a quantity being modelled to be related to whatever explanatory variables are available. Here the "typical value" is more formally a location parameter
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
, which only describes a limited aspect of the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the dependent variable. The GAMLSS approach allows other parameters
Statistical parameter
A statistical parameter is a parameter that indexes a family of probability distributions. It can be regarded as a numerical characteristic of a population or a model....
of the distribution to be related to the explanatory variables; where these other parameters might be interpreted as scale
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
and shape parameter
Shape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
s of the distribution, although the approach is not limited to such parameters.
Overview of the model
The generalized additive model location, scale and shape (GAMLSS) is a statistical model developed by Rigby and Stasinopoulos, and later expanded to overcome some of the limitations associated with the popular generalized linear modelGeneralized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
s (GLMs) and generalized additive model
Generalized additive model
In statistics, the generalized additive model is a statistical model developed by Trevor Hastie and Rob Tibshirani for blending properties of generalized linear models with additive models....
s (GAMs).
In GAMLSS the exponential family
Exponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
assumption for the response variable, (
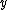), (essential in GLMsGeneralized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
and GAMs
Generalized additive model
In statistics, the generalized additive model is a statistical model developed by Trevor Hastie and Rob Tibshirani for blending properties of generalized linear models with additive models....
), is relaxed and replaced by a general distribution family, including highly skew
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
and/or kurtotic
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
continuous and discrete distributions.
The systematic part of the model is expanded to allow modeling not only of the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
(or location
Location parameter
In statistics, a location family is a class of probability distributions that is parametrized by a scalar- or vector-valued parameter μ, which determines the "location" or shift of the distribution...
) but other parameters of the distribution of y as linear and/or nonlinear, parametric and/or additive non-parametric functions of explanatory variables and/or random effects.
GAMLSS is especially suited for modelling leptokurtic or platykurtic and/or positive or negative skew response variable. For count type response variable data it deals with over-dispersion by using proper over-dispersed discrete distributions. Heterogeneity also is dealt with by modelling the scale
Scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions...
or shape parameter
Shape parameter
In probability theory and statistics, a shape parameter is a kind of numerical parameter of a parametric family of probability distributions.- Definition :...
s using explanatory variables. There are several packages written in R
R (programming language)
R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
related to GAMLSS models.).
A GAMLSS model assumes independent observations
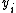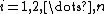
for with probability (density) function
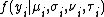conditional on 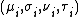a vector of four distribution parameters, each of which can be a function to the explanatory variables. The first two population distribution parameters 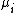and 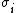are usually characterized as location and scale parameters, while the remaining parameter(s), if any, are characterized as shape parameters, e.g. skewnessSkewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable. The skewness value can be positive or negative, or even undefined...
and kurtosis
Kurtosis
In probability theory and statistics, kurtosis is any measure of the "peakedness" of the probability distribution of a real-valued random variable...
parameters, although the model may be applied more generally to the parameters of any population distribution with up to four distribution parameters, and can be generalized to more than four distribution parameters.
-
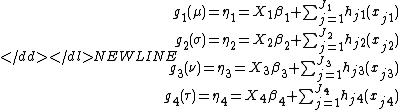
where μ, σ, ν, τ and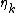
are vectors of length 
, 
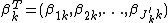is a parameter vector of length 
, 
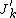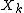is a fixed known design matrix of order 
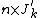and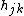 
is a smooth non-parametric function of explanatory variable 
, 
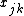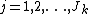and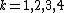 
.
For centile estimation the WHO Multicentre Growth Reference Study Group have recommended GAMLSS and the Box-Cox power exponential (BCPE) distributions for the construction of the WHO Child Growth Standards.
What distributions can be used
The form of the distribution assumed for the response variable y, is very general. For example an implementation of GAMLSS in RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
has around 50 different distributions available. Such implementations also allow use of truncated distributions and censored (or interval) response variables.
Further reading
- Beyerlein, A., Fahrmeir, L., Mansmann, U., Toschke., A. M. (2001) "Alternative regression models to assess increase in childhood BM". IBMC Medical Research Methodology, 2008, 8(59)
- Cole, T. J., Stanojevic, S., Stocks, J., Coates, A. L., Hankinson, J. L., Wade, A. M. (2009), "Age- and size-related reference ranges: A case study of spirometry through childhood and adulthood", Statistics in Medicine, 28(5), 880-898.Link
- Fenske, N., Fahrmeir, L., Rzehak, P., Hohle, M. (25 September 2008), "Detection of risk factors for obesity in early childhood with quantile regression methods for longitudinal data", Department of Statistics: Technical Reports, No.38 Link
- Hudson, I. L., Kim, S. W., Keatley, M. R. (2010), "Climatic Influences on the Flowering Phenology of Four Eucalypts: A GAMLSS Approach Phenological Research". In Phenological Research, Irene L. Hudson and Marie R. Keatley (eds), Springer Netherlands Link
- Hudson, I. L., Rea, A., Dalrymple, M. L., Eilers, P. H. C. (2008), "Climate impacts on sudden infant death syndrome: a GAMLSS approach", Proceedings of the 23rd international workshop on statistical modelling pp. 277–280. Link
- Nott, D. (2006), "Semiparametric estimation of mean and variance functions for non-Gaussian data", Computational Statistics, 21(3-4), 603-620. Link
- Serinaldi, F. (2011), "Distributional modeling and short-term forecasting of electricity prices by Generalized Additive Models for Location, Scale and Shape", Energy Economics, 33(6), 1216-1226,
- Serinaldi, F., Cuomo, G. (2011) "Characterizing impulsive wave-in-deck loads on coastal bridges by probabilistic models of impact maxima and rise times", Coastal Engineering, 58(9), 908-926,
- Serinaldi, F., Villarini, G., Smith, J. A., Krajewski, W. F. (2008), "Change-Point and Trend Analysis on Annual Maximum Discharge in Continental United States", American Geophysical Union Fall Meeting 2008, abstract #H21A-0803*
- van Ogtrop, F. F., Vervoort, R. W. ,Heller, G. Z., Stasinopoulos, D. M., Rigby, R. A. (2011) "Long-range forecasting of intermittent streamflow", Hydrology and Earth System Sciences Discussions, 8(1), 681-713.
- Villarini, G., Serinaldi, F. (2011), "Development of statistical models for at-site probabilistic seasonal rainfall forecast", International Journal of Climatology.
- Villarini, G., Serinaldi, F., Smith, J. A., Krajewski, W. F. (2009), "On the stationarity of annual flood peaks in the continental United States during the 20th century", Water Resources Research, 45(8). Link
- Villarini, G., Smith, J. A., Napolitano, F. (2010), "Nonstationary modeling of a long record of rainfall and temperature over Rome", Advances in Water Resources
External links