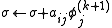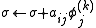Gauss-Seidel method
Encyclopedia
In numerical linear algebra
, the Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method
used to solve a linear system of equations. It is named after the German
mathematician
s Carl Friedrich Gauss
and Philipp Ludwig von Seidel
, and is similar to the Jacobi method
. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is only guaranteed if the matrix is either diagonally dominant
, or symmetric and positive definite
.
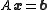
where:
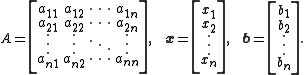
Then A can be decomposed into a lower triangular
component L*, and a strictly upper triangular component U:
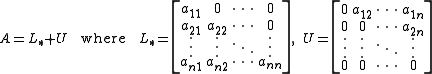
The system of linear equations may be rewritten as:
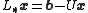
The Gauss–Seidel method is an iterative technique
that solves the left hand side of this expression for x, using previous value for x on the right hand side. Analytically, this may be written as:
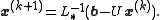
However, by taking advantage of the triangular form of L*, the elements of x(k+1) can be computed sequentially using forward substitution:
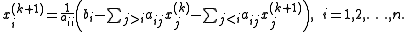
Note that the sum inside this computation of xi(k+1) requires each element in x(k) except xi(k) itself.
The procedure is generally continued until the changes made by an iteration are below some tolerance.
.
The computation of xi(k+1) uses only the elements of x(k+1) that have already been computed, and only the elements of x(k) that have yet to be advanced to iteration k+1. This means that, unlike the Jacobi method, only one storage vector is required as elements can be overwritten as they are computed, which can be advantageous for very large problems.
However, unlike the Jacobi method, the computations for each element cannot be done in parallel
. Furthermore, the values at each iteration are dependent on the order of the original equations.
The Gauss–Seidel method sometimes converges even if these conditions are not satisfied.
Output: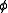
Choose an initial guess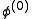 to the solution
to the solution
repeat until convergence
end (repeat)
Gauss-Seidel is the same as SOR (successive over-relaxation)
with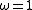 .
.
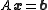 is given by:
is given by:
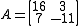 and
and 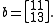
We want to use the equation
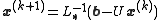
in the form
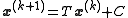
where:
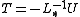 and
and 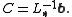
We must decompose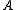 into the sum of a lower triangular component
into the sum of a lower triangular component 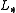 and a strict upper triangular component
and a strict upper triangular component 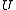 :
:
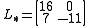 and
and 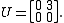
The inverse of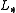 is:
is: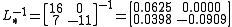 .
.
Now we can find: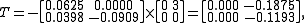
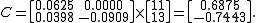
Now we have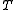 and
and 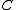 and we can use them to obtain the vectors
and we can use them to obtain the vectors 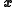 iteratively.
iteratively.
First of all, we have to choose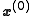 : we can only guess. The better the guess, the quicker the algorithm will perform.
: we can only guess. The better the guess, the quicker the algorithm will perform.
We suppose:
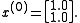
We can then calculate:
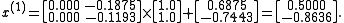
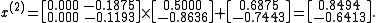
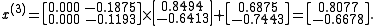
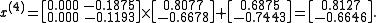
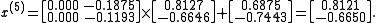
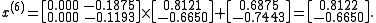
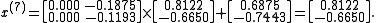
As expected, the algorithm converges to the exact solution:
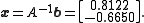
In fact, the matrix A is diagonally dominant (but not positive definite).
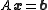 is given by:
is given by:
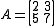 and
and 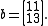
We want to use the equation
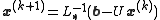
in the form
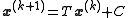
where:
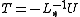 and
and 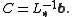
We must decompose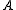 into the sum of a lower triangular component
into the sum of a lower triangular component 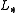 and a strict upper triangular component
and a strict upper triangular component 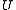 :
:
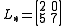 and
and 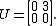
The inverse of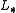 is:
is: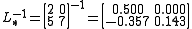 .
.
Now we can find: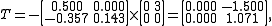
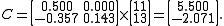
Now we have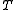 and
and 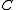 and we can use them to obtain the vectors
and we can use them to obtain the vectors 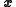 iteratively.
iteratively.
First of all, we have to choose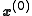 : we can only guess. The better the guess, the quicker will perform the algorithm.
: we can only guess. The better the guess, the quicker will perform the algorithm.
We suppose:
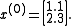
We can then calculate:
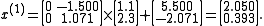
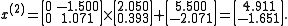
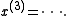
If we test for convergence we'll find that the algorithm diverges. In fact, the matrix A is neither diagonally dominant nor positive definite.
Then, convergence to the exact solution
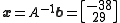
is not guaranteed and, in this case, will not occur.
From the first equation solve for x1 in terms of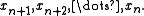 For the next equations substitute the previous values of xs.
For the next equations substitute the previous values of xs.
To make it clear let's consider an example.
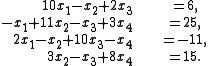
Solving for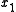 ,
, 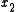 ,
, 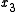 and
and 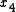 gives:
gives:
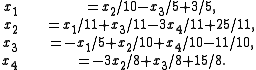
Suppose we choose (0, 0, 0, 0) as the initial approximation, then the first
approximate solution is given by
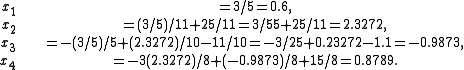
Using the approximations obtained, the iterative procedure is repeated until
the desired accuracy has been reached. The following are the approximated
solutions after four iterations.
{| class="wikitable" border="1"
|-
!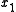
!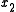
!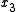
!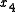
|-
|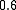
|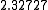
|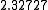
|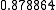
|-
|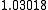
|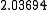
|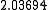
|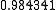
|-
|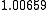
|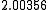
|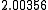
|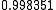
|-
|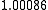
|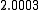
|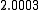
|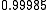
|}
The exact solution of the system is (1, 2, −1, 1).
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, the Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
used to solve a linear system of equations. It is named after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and Philipp Ludwig von Seidel
Philipp Ludwig von Seidel
Philipp Ludwig von Seidel was a German mathematician. His mother was Julie Reinhold and his father was Justus Christian Felix Seidel.Lakatos credits von Seidel with discovering, in 1847, the crucial analytic concept of uniform convergence, while analyzing an incorrect proof of Cauchy's.In 1857,...
, and is similar to the Jacobi method
Jacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
. Though it can be applied to any matrix with non-zero elements on the diagonals, convergence is only guaranteed if the matrix is either diagonally dominant
Diagonally dominant matrix
In mathematics, a matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other entries in that row...
, or symmetric and positive definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
.
Description
Given a square system of n linear equations with unknown x: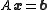
where:
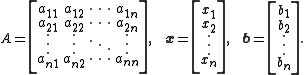
Then A can be decomposed into a lower triangular
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
component L*, and a strictly upper triangular component U:
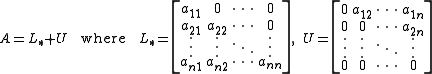
The system of linear equations may be rewritten as:
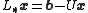
The Gauss–Seidel method is an iterative technique
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
that solves the left hand side of this expression for x, using previous value for x on the right hand side. Analytically, this may be written as:
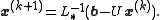
However, by taking advantage of the triangular form of L*, the elements of x(k+1) can be computed sequentially using forward substitution:
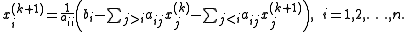
Note that the sum inside this computation of xi(k+1) requires each element in x(k) except xi(k) itself.
The procedure is generally continued until the changes made by an iteration are below some tolerance.
Discussion
The element-wise formula for the Gauss–Seidel method is extremely similar to that of the Jacobi methodJacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
.
The computation of xi(k+1) uses only the elements of x(k+1) that have already been computed, and only the elements of x(k) that have yet to be advanced to iteration k+1. This means that, unlike the Jacobi method, only one storage vector is required as elements can be overwritten as they are computed, which can be advantageous for very large problems.
However, unlike the Jacobi method, the computations for each element cannot be done in parallel
Parallel algorithm
In computer science, a parallel algorithm or concurrent algorithm, as opposed to a traditional sequential algorithm, is an algorithm which can be executed a piece at a time on many different processing devices, and then put back together again at the end to get the correct result.Some algorithms...
. Furthermore, the values at each iteration are dependent on the order of the original equations.
Convergence
The convergence properties of the Gauss–Seidel method are dependent on the matrix A. Namely, the procedure is known to converge if either:- A is symmetric positive-definitePositive-definite matrixIn linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, or - A is strictly or irreducibly diagonally dominantDiagonally dominant matrixIn mathematics, a matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other entries in that row...
.
The Gauss–Seidel method sometimes converges even if these conditions are not satisfied.
Algorithm
Inputs: A , bOutput:
Choose an initial guess
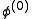 to the solution
to the solution repeat until convergence
- for i from 1 until n do
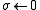
- for j from 1 until i-1 do
- end (j-loop)
- for j from i + 1 until n do
- end (j-loop)
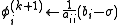
- end (i-loop)
- check if convergence is reached
end (repeat)
Gauss-Seidel is the same as SOR (successive over-relaxation)
Successive over-relaxation
In numerical linear algebra, the method of successive over-relaxation is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process.It was devised simultaneously by David...
with
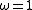 .
.An example for the matrix version
A linear system shown as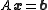 is given by:
is given by: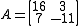 and
and 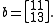
We want to use the equation
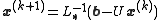
in the form
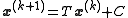
where:
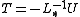 and
and 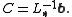
We must decompose
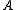 into the sum of a lower triangular component
into the sum of a lower triangular component 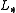 and a strict upper triangular component
and a strict upper triangular component 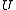 :
: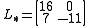 and
and 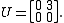
The inverse of
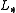 is:
is: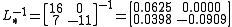 .
.Now we can find:
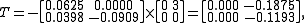
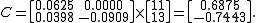
Now we have
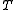 and
and 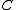 and we can use them to obtain the vectors
and we can use them to obtain the vectors 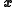 iteratively.
iteratively.First of all, we have to choose
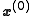 : we can only guess. The better the guess, the quicker the algorithm will perform.
: we can only guess. The better the guess, the quicker the algorithm will perform.We suppose:
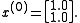
We can then calculate:
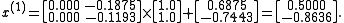
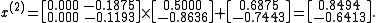
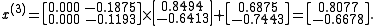
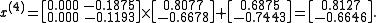
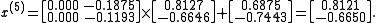
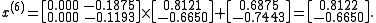
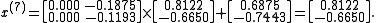
As expected, the algorithm converges to the exact solution:
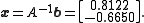
In fact, the matrix A is diagonally dominant (but not positive definite).
Another example for the matrix version
Another linear system shown as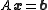 is given by:
is given by: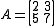 and
and 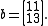
We want to use the equation
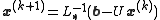
in the form
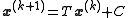
where:
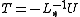 and
and 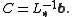
We must decompose
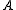 into the sum of a lower triangular component
into the sum of a lower triangular component 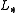 and a strict upper triangular component
and a strict upper triangular component 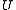 :
: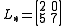 and
and 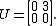
The inverse of
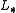 is:
is: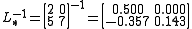 .
.Now we can find:
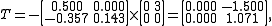
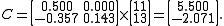
Now we have
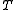 and
and 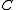 and we can use them to obtain the vectors
and we can use them to obtain the vectors 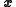 iteratively.
iteratively.First of all, we have to choose
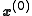 : we can only guess. The better the guess, the quicker will perform the algorithm.
: we can only guess. The better the guess, the quicker will perform the algorithm.We suppose:
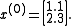
We can then calculate:
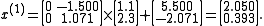
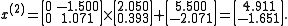
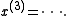
If we test for convergence we'll find that the algorithm diverges. In fact, the matrix A is neither diagonally dominant nor positive definite.
Then, convergence to the exact solution
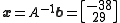
is not guaranteed and, in this case, will not occur.
An example for the equation version
Suppose given k equations where xn are vectors of these equations and starting point x0.From the first equation solve for x1 in terms of
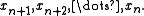 For the next equations substitute the previous values of xs.
For the next equations substitute the previous values of xs.To make it clear let's consider an example.
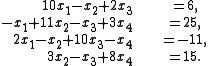
Solving for
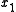 ,
, 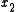 ,
, 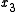 and
and 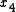 gives:
gives: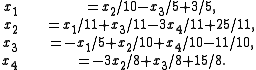
Suppose we choose (0, 0, 0, 0) as the initial approximation, then the first
approximate solution is given by
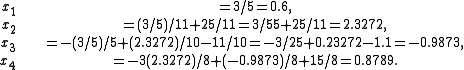
Using the approximations obtained, the iterative procedure is repeated until
the desired accuracy has been reached. The following are the approximated
solutions after four iterations.
{| class="wikitable" border="1"
|-
!
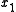
!
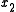
!
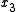
!
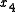
|-
|
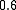
|
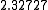
|
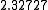
|
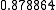
|-
|
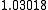
|
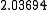
|
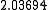
|
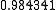
|-
|
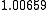
|
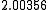
|
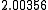
|
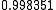
|-
|
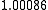
|
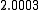
|
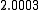
|
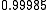
|}
The exact solution of the system is (1, 2, −1, 1).
See also
- Jacobi methodJacobi methodIn numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
- Successive over-relaxationSuccessive over-relaxationIn numerical linear algebra, the method of successive over-relaxation is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process.It was devised simultaneously by David...
- Iterative method. Linear systems
- Gaussian belief propagation
External links
- Gauss–Seidel from www.math-linux.com
- Module for Gauss–Seidel Iteration
- Gauss–Seidel From Holistic Numerical Methods Institute
- Gauss Siedel Iteration from www.geocities.com
- The Gauss-Seidel Method
- Bickson
- Matlab code
- C code example