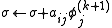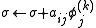Successive over-relaxation
Encyclopedia
In numerical linear algebra
, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process
.
It was devised simultaneously by David M. Young, Jr.
and by H. Frankel in 1950 for the purpose of automatically solving linear systems on digital computers. Over-relaxation methods had been used before the work of Young and Frankel. For instance, the method of Lewis Fry Richardson
, and the methods developed by R. V. Southwell
. However, these methods were designed for computation by human calculators, and they required some expertise to ensure convergence to the solution which made them inapplicable for programming on digital computers. These aspects are discussed in the thesis of David M. Young, Jr..
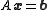
where:
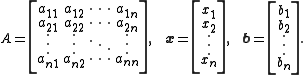
Then A can be decomposed into a diagonal
component D, and strictly lower and upper triangular components L and U:
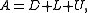
where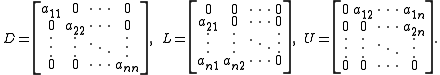
The system of linear equations may be rewritten as:
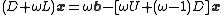
for a constant ω > 1.
The method of successive over-relaxation is an iterative technique
that solves the left hand side of this expression for x, using previous value for x on the right hand side. Analytically, this may be written as:
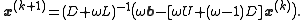
However, by taking advantage of the triangular form of (D+ωL), the elements of x(k+1) can be computed sequentially using forward substitution:
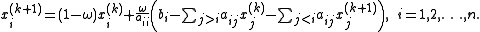
The choice of relaxation factor is not necessarily easy, and depends upon the properties of the coefficient matrix. For symmetric, positive-definite
matrices
it can be proven that 0 < ω < 2 will lead to convergence, but we are generally interested in faster convergence rather than just convergence.
Output: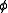
Choose an initial guess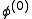 to the solution
to the solution
repeat until convergence
end (repeat)
Note:
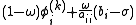 can also be written
can also be written 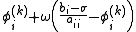 , thus saving one multiplication in each iteration of the outer for-loop.
, thus saving one multiplication in each iteration of the outer for-loop.
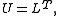
is referred to as Symmetric Successive Over Relaxation, or (SSOR), in which
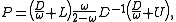
and the iterative method is
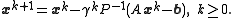
The SOR and SSOR methods are credited to David M. Young, Jr.
.
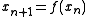
then the modified version would use
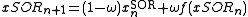
or equivalently
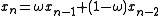
Values of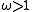 are used to speedup convergence of a slow-converging process, while values of
are used to speedup convergence of a slow-converging process, while values of 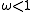 are often used to help establish convergence of a diverging iterative process.
are often used to help establish convergence of a diverging iterative process.
There are various methods that adaptively set the relaxation parameter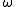 based on the observed behavior of the converging process. Usually they help to reach a super-linear convergence for some problems but fail for the others.
based on the observed behavior of the converging process. Usually they help to reach a super-linear convergence for some problems but fail for the others.
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, the method of successive over-relaxation (SOR) is a variant of the Gauss–Seidel method for solving a linear system of equations, resulting in faster convergence. A similar method can be used for any slowly converging iterative process
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
.
It was devised simultaneously by David M. Young, Jr.
David M. Young, Jr.
David M. Young, Jr. was an American mathematician and computer scientist who was one of the pioneers in the field of modern numerical analysis/scientific computing....
and by H. Frankel in 1950 for the purpose of automatically solving linear systems on digital computers. Over-relaxation methods had been used before the work of Young and Frankel. For instance, the method of Lewis Fry Richardson
Lewis Fry Richardson
Lewis Fry Richardson, FRS was an English mathematician, physicist, meteorologist, psychologist and pacifist who pioneered modern mathematical techniques of weather forecasting, and the application of similar techniques to studying the causes of wars and how to prevent them...
, and the methods developed by R. V. Southwell
Richard V. Southwell
Sir Richard Vynne Southwell MA, LLD, FRS was a British mathematician who specialized in applied mechanics as an engineering science academic.- Education and career :...
. However, these methods were designed for computation by human calculators, and they required some expertise to ensure convergence to the solution which made them inapplicable for programming on digital computers. These aspects are discussed in the thesis of David M. Young, Jr..
Formulation
Given a square system of n linear equations with unknown x: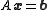
where:
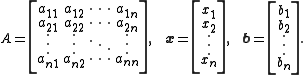
Then A can be decomposed into a diagonal
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
component D, and strictly lower and upper triangular components L and U:
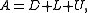
where
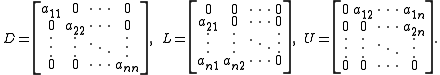
The system of linear equations may be rewritten as:
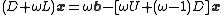
for a constant ω > 1.
The method of successive over-relaxation is an iterative technique
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
that solves the left hand side of this expression for x, using previous value for x on the right hand side. Analytically, this may be written as:
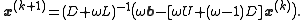
However, by taking advantage of the triangular form of (D+ωL), the elements of x(k+1) can be computed sequentially using forward substitution:
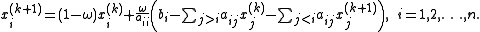
The choice of relaxation factor is not necessarily easy, and depends upon the properties of the coefficient matrix. For symmetric, positive-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
it can be proven that 0 < ω < 2 will lead to convergence, but we are generally interested in faster convergence rather than just convergence.
Algorithm
Inputs: A , b, ωOutput:
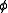
Choose an initial guess
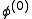 to the solution
to the solution repeat until convergence
- for i from 1 until n do
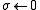
- for j from 1 until i − 1 do
- end (j-loop)
- for j from i + 1 until n do
- end (j-loop)
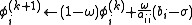
- end (i-loop)
- check if convergence is reached
end (repeat)
Note:
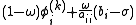 can also be written
can also be written 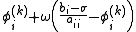 , thus saving one multiplication in each iteration of the outer for-loop.
, thus saving one multiplication in each iteration of the outer for-loop.Symmetric Successive Over Relaxation
The version for symmetric matrices A, in which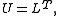
is referred to as Symmetric Successive Over Relaxation, or (SSOR), in which
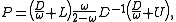
and the iterative method is
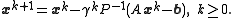
The SOR and SSOR methods are credited to David M. Young, Jr.
David M. Young, Jr.
David M. Young, Jr. was an American mathematician and computer scientist who was one of the pioneers in the field of modern numerical analysis/scientific computing....
.
Other applications of the method
A similar technique can be used for any iterative method. If the original iteration had the form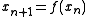
then the modified version would use
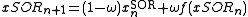
or equivalently
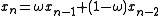
Values of
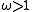 are used to speedup convergence of a slow-converging process, while values of
are used to speedup convergence of a slow-converging process, while values of 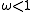 are often used to help establish convergence of a diverging iterative process.
are often used to help establish convergence of a diverging iterative process.There are various methods that adaptively set the relaxation parameter
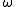 based on the observed behavior of the converging process. Usually they help to reach a super-linear convergence for some problems but fail for the others.
based on the observed behavior of the converging process. Usually they help to reach a super-linear convergence for some problems but fail for the others.See also
- Jacobi methodJacobi methodIn numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
- Gaussian Belief Propagation