
G-networks
Encyclopedia
In queueing theory
, a discipline within the mathematical theory of probability
, a G–network (generalized queueing network or Gelenbe network) is an open network of G–queues first introduced by Erol Gelenbe
as a model for queueing systems with specific control functions, such as traffic re-routing or traffic destruction, as well as a model for neural networks
. A G–queue is a network of queues with several types of novel and useful customers:
A product form solution
superficially similar in form to Jackson's theorem, but which requires the solution of a system of non-linear equations for the traffic flows, exists for the stationary distribution of G–networks while the traffic equations of a G–network are in fact surprisingly non-linear, and the model does not obey partial balance. This broke previous assumptions that partial balance was a necessary condition for a product form solution. A powerful property of G–networks is that they are universal approximators for continuous and bounded functions, so that they can be used to approximate quite general input-output behaviours.
A queue in such a network is known as a G–queue.
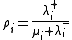
where the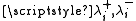 for
for 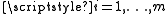 satisfy
satisfy
Then writing (n1, … ,nm) for the state of the network (with queue length ni at node i), if a unique non-negative solution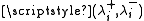 exists to the above equations and such that ρi for all i then the stationary probability distribution π exists and is given by
exists to the above equations and such that ρi for all i then the stationary probability distribution π exists and is given by
 satisfies the global balance equations
satisfies the global balance equations
which, quite differently from Jackson networks are non-linear. We note that the model also allows for multiple classes.
G–networks have been used in a wide range of applications, including to represent Gene Regulatory Networks, the mix of control and payload in packet networks, neural networks, and the representation of colour images and medical images such as Magnetic Resonance Images.
where λ = λ+ + λ− and ρ = λ+/(λ− + μ), requiring ρ < 1 for stability.
The response time for a tandem pair of G–queues (where customers who finish service at the first node immediately move to the second, then leave the network) is also known, and it is thought extensions to larger networks will be intractable.
Queueing theory
Queueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
, a discipline within the mathematical theory of probability
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a G–network (generalized queueing network or Gelenbe network) is an open network of G–queues first introduced by Erol Gelenbe
Erol Gelenbe
Sami Erol Gelenbe is a Turkish computer scientist, engineer and applied mathematician who currently holds the Dennis Gabor Professorship at Imperial College...
as a model for queueing systems with specific control functions, such as traffic re-routing or traffic destruction, as well as a model for neural networks
Neural Networks
Neural Networks is the official journal of the three oldest societies dedicated to research in neural networks: International Neural Network Society, European Neural Network Society and Japanese Neural Network Society, published by Elsevier...
. A G–queue is a network of queues with several types of novel and useful customers:
- positive customers, which arrive from other queues or arrive externally as Poisson arrivals, and obey standard service and routing disciplines as in conventional network models,
- negative customers, which arrive from another queue, or which arrive externally as Poisson arrivals, and remove (or 'kill') customers in a non-empty queue, representing the need to remove traffic when the network is congested, including the removal of "batches" of customers
- "triggers", which arrive from other queues or from outside the network, and which displace customers and move them to other queues
A product form solution
Product form solution
In probability theory, a product form solution is a particularly efficient form of solution for determining some metric of a system with distinct sub-components, where the metric for the collection of components can be written as a product of the metric across the different components...
superficially similar in form to Jackson's theorem, but which requires the solution of a system of non-linear equations for the traffic flows, exists for the stationary distribution of G–networks while the traffic equations of a G–network are in fact surprisingly non-linear, and the model does not obey partial balance. This broke previous assumptions that partial balance was a necessary condition for a product form solution. A powerful property of G–networks is that they are universal approximators for continuous and bounded functions, so that they can be used to approximate quite general input-output behaviours.
Definition
A network of m interconnected queues is a G–network if- each queue has one server, who serves at rate μi,
- external arrivals of positive customers or of triggers or resets form Poisson processes of rate
 for positive customers, while triggers and resets, including negative customers, form a Poisson process of rate
for positive customers, while triggers and resets, including negative customers, form a Poisson process of rate  ,
, - on completing service a customer moves from queue i to queue j as a positive customer with probability
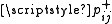 , as a trigger or reset with probability
, as a trigger or reset with probability 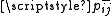 and departs the network with probability
and departs the network with probability 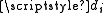 ,
, - on arrival to a queue, a positive customer acts as usual and increases the queue length by 1,
- on arrival to a queue, the negative customer reduces the length of the queue by some random number (if there is at least one positive customer present at the queue), while a trigger moves a customer probabilistically to another queue and a reset sets the state of the queue to its steady-state if the queue is empty when the reset arrives. All triggers, negative customers and resets disapper after they have taken their action, so that they are in fact "control" signals in the network,
- note that normal customers leaving a queue can become triggers or resets and negative customers when they visit the next queue.
A queue in such a network is known as a G–queue.
Stationary distribution
Define the utilization at each node,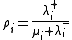
where the
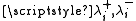 for
for 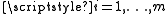 satisfy
satisfyThen writing (n1, … ,nm) for the state of the network (with queue length ni at node i), if a unique non-negative solution
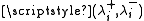 exists to the above equations and such that ρi for all i then the stationary probability distribution π exists and is given by
exists to the above equations and such that ρi for all i then the stationary probability distribution π exists and is given by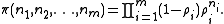
Proof
It is sufficient to show satisfies the global balance equations
satisfies the global balance equationsBalance equation
In probability theory, a balance equation is an equation that describes the probability flux associated with a Markov chain in and out of states or set of states.-Global balance:...
which, quite differently from Jackson networks are non-linear. We note that the model also allows for multiple classes.
G–networks have been used in a wide range of applications, including to represent Gene Regulatory Networks, the mix of control and payload in packet networks, neural networks, and the representation of colour images and medical images such as Magnetic Resonance Images.
Response time distribution
The response time is the length of time a customer spends in the system. The response time distribution for a single G–queue is known where customers are served using a FCFS discipline at rate μ, with positive arrivals at rate λ+ and negative arrivals at rate λ− which kill customers from the end of the queue. The Laplace transform of response time distribution in this situation is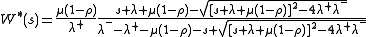
where λ = λ+ + λ− and ρ = λ+/(λ− + μ), requiring ρ < 1 for stability.
The response time for a tandem pair of G–queues (where customers who finish service at the first node immediately move to the second, then leave the network) is also known, and it is thought extensions to larger networks will be intractable.

