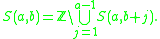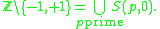Furstenberg's proof of the infinitude of primes
Encyclopedia
In number theory
, Hillel Fürstenberg's proof of the infinitude of primes is a celebrated topological
proof
that the integer
s contain infinitely many prime number
s. When examined closely, the proof is less a statement about topology than a statement about certain properties of arithmetic sequences. Unlike Euclid's classical proof, Fürstenberg's is a proof by contradiction. The proof was published in 1955 in the American Mathematical Monthly
while Fürstenberg was still an undergraduate student at Yeshiva University
.
if and only if
it is either the empty set
, ∅, or it is a union
of arithmetic sequences S(a, b) (for a ≠ 0), where
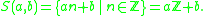
In other words, U is open if and only if every x ∈ U admits some non-zero integer a such that S(a, x) ⊆ U. The axioms for a topology
are easily verified:
The topology is quite different from the usual Euclidean one, and has two notable properties:
The only integers that are not integer multiples of prime numbers are −1 and +1, i.e.
By the first property, the set on the left-hand side cannot be closed. On the other hand, by the second property, the sets S(p, 0) are closed. So, if there were only finitely many prime numbers, then the set on the right-hand side would be a finite union of closed sets, and hence closed. This would be a contradiction
, so there must be infinitely many prime numbers.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Hillel Fürstenberg's proof of the infinitude of primes is a celebrated topological
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s contain infinitely many prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. When examined closely, the proof is less a statement about topology than a statement about certain properties of arithmetic sequences. Unlike Euclid's classical proof, Fürstenberg's is a proof by contradiction. The proof was published in 1955 in the American Mathematical Monthly
American Mathematical Monthly
The American Mathematical Monthly is a mathematical journal founded by Benjamin Finkel in 1894. It is currently published 10 times each year by the Mathematical Association of America....
while Fürstenberg was still an undergraduate student at Yeshiva University
Yeshiva University
Yeshiva University is a private university in New York City, with six campuses in New York and one in Israel. Founded in 1886, it is a research university ranked as 45th in the US among national universities by U.S. News & World Report in 2012...
.
Fürstenberg's proof
Define a topology on the integers Z, called the evenly spaced integer topology, by declaring a subset U ⊆ Z to be an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is either the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, ∅, or it is a union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of arithmetic sequences S(a, b) (for a ≠ 0), where
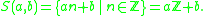
In other words, U is open if and only if every x ∈ U admits some non-zero integer a such that S(a, x) ⊆ U. The axioms for a topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
are easily verified:
- By definition, ∅ is open; Z is just the sequence S(1, 0), and so is open as well.
- Any union of open sets is open: for any collection of open sets Ui and x in their union U, any of the numbers ai for which S(ai, x) ⊆ Ui also shows that S(ai, x) ⊆ U.
- The intersection of two (and hence finitely many) open sets is open: let U1 and U2 be open sets and let x ∈ U1 ∩ U2 (with numbers a1 and a2 establishing membership). Set a to be the lowest common multiple of a1 and a2. Then S(a, x) ⊆ S(ai, x) ⊆ Ui.
The topology is quite different from the usual Euclidean one, and has two notable properties:
- Since any non-empty open set contains an infinite sequence, no finite set can be open; put another way, the complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of a finite set cannot be a closed setClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
. - The basis sets S(a, b) are both open and closedClopen setIn topology, a clopen set in a topological space is a set which is both open and closed. That this is possible for a set is not as counter-intuitive as it might seem if the terms open and closed were thought of as antonyms; in fact they are not...
: they are open by definition, and we can write S(a, b) as the complement of an open set as follows:
The only integers that are not integer multiples of prime numbers are −1 and +1, i.e.
By the first property, the set on the left-hand side cannot be closed. On the other hand, by the second property, the sets S(p, 0) are closed. So, if there were only finitely many prime numbers, then the set on the right-hand side would be a finite union of closed sets, and hence closed. This would be a contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
, so there must be infinitely many prime numbers.
External links
- Fürstenberg's proof that there are infinitely many prime numbers at Everything2Everything2Everything2, Everything2, or E2 for short is a collaborative Web-based community consisting of a database of interlinked user-submitted written material. E2 is moderated for quality, but has no formal policy on subject matter...