
Fundamental theorems of welfare economics
Encyclopedia
There are two fundamental theorems of welfare economics
. The first states that any competitive equilibrium
or Walrasian equilibrium leads to a Pareto efficient
allocation of resources. The second states the converse, that any efficient allocation can be sustainable by a competitive equilibrium. Despite the apparent symmetry of the two theorems, in fact the first theorem is much more general than the second, requiring far weaker assumptions.
The first theorem is often taken to be an analytical confirmation of Adam Smith
's "invisible hand
" hypothesis, namely that competitive markets tend toward an efficient allocation of resources. The theorem supports a case for non-intervention in ideal conditions: let the markets do the work and the outcome will be Pareto efficient. However, Pareto efficiency is not necessarily the same thing as desirability; it merely indicates that no one can be made better off without someone being made worse off. There can be many possible Pareto efficient allocations of resources and not all of them may be equally desirable by society.
The ideal conditions of the theorems, however are an abstraction. The Greenwald-Stiglitz theorem, for example, states that in the presence of either imperfect information, or incomplete markets, markets are not Pareto efficient. Thus, in most real world economies, the degree of these variations from ideal conditions must factor into policy choices.
The second theorem states that out of all possible Pareto efficient outcomes one can achieve any particular one by enacting a lump-sum wealth redistribution and then letting the market take over. This appears to make the case that intervention has a legitimate place in policy – redistributions can allow us to select from all efficient outcomes for one that has other desired features, such as distributional equity. The shortcoming is that for the theorem to hold, the transfers have to be lump-sum and the government needs to have perfect information on individual consumers' tastes as well as the production possibilities of firms. Additionally, an additional mathematical condition is that preferences and production technologies have to be convex
.
. This was first demonstrated graphically by economist Abba Lerner and mathematically by economists Harold Hotelling
, Oskar Lange
, Maurice Allais
, Kenneth Arrow
and Gerard Debreu
. The theorem holds under general conditions. The only assumption needed (in addition to complete market
s and price-taking behavior) is the relatively weak assumption of local nonsatiation of preferences
. In particular, no convexity
assumptions are needed.
 is convex
is convex
and every preference relation is convex and locally nonsatiated
is convex and locally nonsatiated
, any desired Pareto-efficient allocation can be supported as a price quasi-equilibrium with transfers. Further assumptions are needed to prove this statement for price equilibriums with transfers. We will proceed in two steps: first we prove that any Pareto-efficient allocation can be supported as a price quasi-equilibrium with transfers, then we give conditions under which a price quasi-equilibrium is also a price equilibrium.
Let us define a price quasi-equilibrium with transfers as an allocation , a price vector p, and a vector of wealth levels w (achieved by lump-sum transfers) with
, a price vector p, and a vector of wealth levels w (achieved by lump-sum transfers) with  (where
(where 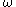 is the aggregate endowment of goods and
is the aggregate endowment of goods and  is the production of firm j) such that:
is the production of firm j) such that:
The only difference between this definition and the standard definition of a price equilibrium with transfers is in statement (ii). The inequality is weak here ( ) making it a price quasi-equilibrium. Later we will strengthen this to make a price equilibrium.
) making it a price quasi-equilibrium. Later we will strengthen this to make a price equilibrium.
Define to be the set of all consumption bundles strictly preferred to
to be the set of all consumption bundles strictly preferred to  by consumer i, and let V be the sum of all
by consumer i, and let V be the sum of all 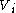 .
.  is convex due to the convexity of the preference relation
is convex due to the convexity of the preference relation 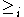 . V is convex because every
. V is convex because every 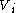 is convex. Similarly
is convex. Similarly  , the union of all production sets
, the union of all production sets  plus the aggregate endowment, is convex because every
plus the aggregate endowment, is convex because every  is convex. We also know that the intersection of V and
is convex. We also know that the intersection of V and  must be empty, because if it were not it would imply there existed a bundle that is strictly preferred to
must be empty, because if it were not it would imply there existed a bundle that is strictly preferred to  by everyone and is also affordable. This is ruled out by the Pareto-optimality of
by everyone and is also affordable. This is ruled out by the Pareto-optimality of 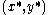 .
.
These two convex, non-intersecting sets allow us to apply the separating hyperplane theorem. This theorem states that there exists a price vector and a number r such that
and a number r such that 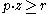 for every
for every  and
and  for every
for every 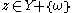 . In other words, there exists a price vector that defines a hyperplane that perfectly separates the two convex sets.
. In other words, there exists a price vector that defines a hyperplane that perfectly separates the two convex sets.
Next we argue that if for all i then
for all i then  . This is due to local nonsatiation: there must be a bundle
. This is due to local nonsatiation: there must be a bundle 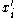 arbitrarily close to
arbitrarily close to  that is strictly preferred to
that is strictly preferred to  and hence part of
and hence part of  , so
, so  . Taking the limit as
. Taking the limit as  does not change the weak inequality, so
does not change the weak inequality, so  as well. In other words,
as well. In other words,  is in the closure
is in the closure
of V.
Using this relation we see that for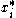 itself
itself  . We also know that
. We also know that  , so
, so  as well. Combining these we find that
as well. Combining these we find that  . We can use this equation to show that
. We can use this equation to show that  fits the definition of a price quasi-equilibrium with transfers.
fits the definition of a price quasi-equilibrium with transfers.
Because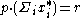 and
and 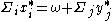 we know that for any firm j:
we know that for any firm j:
which implies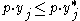 . Similarly we know:
. Similarly we know:
which implies . These two statements, along with the feasibility of the allocation at the Pareto optimum, satisfy the three conditions for a price quasi-equilibrium with transfers supported by wealth levels
. These two statements, along with the feasibility of the allocation at the Pareto optimum, satisfy the three conditions for a price quasi-equilibrium with transfers supported by wealth levels  for all i.
for all i.
We now turn to conditions under which a price quasi-equilibrium is also a price equilibrium, in other words, conditions under which the statement "if then
then  " imples "if
" imples "if  then
then  ". For this to be true we need now to assume that the consumption set
". For this to be true we need now to assume that the consumption set  is convex and the preference relation
is convex and the preference relation  is continuous
is continuous
. Then, if there exists a consumption vector such that
such that 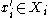 and
and  , a price quasi-equilibrium is a price equilibrium.
, a price quasi-equilibrium is a price equilibrium.
To see why, assume to the contrary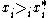 and
and 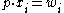 , and
, and  exists. Then by the convexity of
exists. Then by the convexity of  we have a bundle
we have a bundle 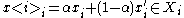 with
with  . By the continuity of
. By the continuity of  for
for  close to 1 we have
close to 1 we have  . This is a contradiction, because this bundle is preferred to
. This is a contradiction, because this bundle is preferred to  and costs less than
and costs less than  .
.
Hence, for price quasi-equilibria to be price equilibria it is sufficient that the consumption set be convex, the preference relation to be continuous, and for there always to exist a "cheaper" consumption bundle . One way to ensure the existence of such a bundle is to require wealth levels
. One way to ensure the existence of such a bundle is to require wealth levels  to be strictly positive for all consumers i.
to be strictly positive for all consumers i.
Welfare economics
Welfare economics is a branch of economics that uses microeconomic techniques to evaluate economic well-being, especially relative to competitive general equilibrium within an economy as to economic efficiency and the resulting income distribution associated with it...
. The first states that any competitive equilibrium
Competitive equilibrium
Competitive market equilibrium is the traditional concept of economic equilibrium, appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis...
or Walrasian equilibrium leads to a Pareto efficient
Pareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
allocation of resources. The second states the converse, that any efficient allocation can be sustainable by a competitive equilibrium. Despite the apparent symmetry of the two theorems, in fact the first theorem is much more general than the second, requiring far weaker assumptions.
The first theorem is often taken to be an analytical confirmation of Adam Smith
Adam Smith
Adam Smith was a Scottish social philosopher and a pioneer of political economy. One of the key figures of the Scottish Enlightenment, Smith is the author of The Theory of Moral Sentiments and An Inquiry into the Nature and Causes of the Wealth of Nations...
's "invisible hand
Invisible hand
In economics, invisible hand or invisible hand of the market is the term economists use to describe the self-regulating nature of the marketplace. This is a metaphor first coined by the economist Adam Smith...
" hypothesis, namely that competitive markets tend toward an efficient allocation of resources. The theorem supports a case for non-intervention in ideal conditions: let the markets do the work and the outcome will be Pareto efficient. However, Pareto efficiency is not necessarily the same thing as desirability; it merely indicates that no one can be made better off without someone being made worse off. There can be many possible Pareto efficient allocations of resources and not all of them may be equally desirable by society.
The ideal conditions of the theorems, however are an abstraction. The Greenwald-Stiglitz theorem, for example, states that in the presence of either imperfect information, or incomplete markets, markets are not Pareto efficient. Thus, in most real world economies, the degree of these variations from ideal conditions must factor into policy choices.
The second theorem states that out of all possible Pareto efficient outcomes one can achieve any particular one by enacting a lump-sum wealth redistribution and then letting the market take over. This appears to make the case that intervention has a legitimate place in policy – redistributions can allow us to select from all efficient outcomes for one that has other desired features, such as distributional equity. The shortcoming is that for the theorem to hold, the transfers have to be lump-sum and the government needs to have perfect information on individual consumers' tastes as well as the production possibilities of firms. Additionally, an additional mathematical condition is that preferences and production technologies have to be convex
Convex
'The word convex means curving out or bulging outward, as opposed to concave. Convex or convexity may refer to:Mathematics:* Convex set, a set of points containing all line segments between each pair of its points...
.
Proof of the first fundamental theorem
The "First fundamental theorem of welfare economics" states that any Walrasian equilibrium is Pareto-efficientPareto efficiency
Pareto efficiency, or Pareto optimality, is a concept in economics with applications in engineering and social sciences. The term is named after Vilfredo Pareto, an Italian economist who used the concept in his studies of economic efficiency and income distribution.Given an initial allocation of...
. This was first demonstrated graphically by economist Abba Lerner and mathematically by economists Harold Hotelling
Harold Hotelling
Harold Hotelling was a mathematical statistician and an influential economic theorist.He was Associate Professor of Mathematics at Stanford University from 1927 until 1931, a member of the faculty of Columbia University from 1931 until 1946, and a Professor of Mathematical Statistics at the...
, Oskar Lange
Oskar Lange
Oskar Ryszard Lange was a Polish economist and diplomat...
, Maurice Allais
Maurice Allais
Maurice Félix Charles Allais was a French economist, and was the 1988 winner of the Nobel Memorial Prize in Economics "for his pioneering contributions to the theory of markets and efficient utilization of resources."...
, Kenneth Arrow
Kenneth Arrow
Kenneth Joseph Arrow is an American economist and joint winner of the Nobel Memorial Prize in Economics with John Hicks in 1972. To date, he is the youngest person to have received this award, at 51....
and Gerard Debreu
Gerard Debreu
Gérard Debreu was a French economist and mathematician, who also came to have United States citizenship. Best known as a professor of economics at the University of California, Berkeley, where he began work in 1962, he won the 1983 Nobel Memorial Prize in Economics.-Biography:His father was the...
. The theorem holds under general conditions. The only assumption needed (in addition to complete market
Complete market
In economics, a complete market is one in which the complete set of possible gambles on future states-of-the-world can be constructed with existing assets without friction. Every agent is able to exchange every good, directly or indirectly, with every other agent without transaction costs...
s and price-taking behavior) is the relatively weak assumption of local nonsatiation of preferences
Local nonsatiation
The property of local nonsatiation of consumer preferences states that for any bundle of goods there is always another bundle of goods arbitrarily close that is preferred to it....
. In particular, no convexity
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
assumptions are needed.
Proof of the second fundamental theorem
The second fundamental theorem of welfare economics states that, under the assumptions that every production set is convex
is convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
and every preference relation
 is convex and locally nonsatiated
is convex and locally nonsatiatedLocal nonsatiation
The property of local nonsatiation of consumer preferences states that for any bundle of goods there is always another bundle of goods arbitrarily close that is preferred to it....
, any desired Pareto-efficient allocation can be supported as a price quasi-equilibrium with transfers. Further assumptions are needed to prove this statement for price equilibriums with transfers. We will proceed in two steps: first we prove that any Pareto-efficient allocation can be supported as a price quasi-equilibrium with transfers, then we give conditions under which a price quasi-equilibrium is also a price equilibrium.
Let us define a price quasi-equilibrium with transfers as an allocation
 , a price vector p, and a vector of wealth levels w (achieved by lump-sum transfers) with
, a price vector p, and a vector of wealth levels w (achieved by lump-sum transfers) with  (where
(where 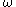 is the aggregate endowment of goods and
is the aggregate endowment of goods and  is the production of firm j) such that:
is the production of firm j) such that:-
- i.
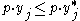 for all
for all 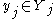 (firms maximize profit by producing
(firms maximize profit by producing 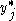 )
) - ii. For all i, if
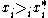 then
then 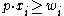 (if
(if 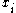 is strictly preferred to
is strictly preferred to  then it cannot cost less than
then it cannot cost less than 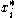 )
) - iii.
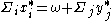 (budget constraint satisfied)
(budget constraint satisfied)
- i.
The only difference between this definition and the standard definition of a price equilibrium with transfers is in statement (ii). The inequality is weak here (
 ) making it a price quasi-equilibrium. Later we will strengthen this to make a price equilibrium.
) making it a price quasi-equilibrium. Later we will strengthen this to make a price equilibrium.Define
 to be the set of all consumption bundles strictly preferred to
to be the set of all consumption bundles strictly preferred to  by consumer i, and let V be the sum of all
by consumer i, and let V be the sum of all 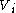 .
.  is convex due to the convexity of the preference relation
is convex due to the convexity of the preference relation 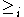 . V is convex because every
. V is convex because every 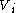 is convex. Similarly
is convex. Similarly  , the union of all production sets
, the union of all production sets  plus the aggregate endowment, is convex because every
plus the aggregate endowment, is convex because every  is convex. We also know that the intersection of V and
is convex. We also know that the intersection of V and  must be empty, because if it were not it would imply there existed a bundle that is strictly preferred to
must be empty, because if it were not it would imply there existed a bundle that is strictly preferred to  by everyone and is also affordable. This is ruled out by the Pareto-optimality of
by everyone and is also affordable. This is ruled out by the Pareto-optimality of 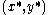 .
.These two convex, non-intersecting sets allow us to apply the separating hyperplane theorem. This theorem states that there exists a price vector
 and a number r such that
and a number r such that 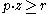 for every
for every  and
and  for every
for every 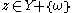 . In other words, there exists a price vector that defines a hyperplane that perfectly separates the two convex sets.
. In other words, there exists a price vector that defines a hyperplane that perfectly separates the two convex sets.Next we argue that if
 for all i then
for all i then  . This is due to local nonsatiation: there must be a bundle
. This is due to local nonsatiation: there must be a bundle 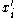 arbitrarily close to
arbitrarily close to  that is strictly preferred to
that is strictly preferred to  and hence part of
and hence part of  , so
, so  . Taking the limit as
. Taking the limit as  does not change the weak inequality, so
does not change the weak inequality, so  as well. In other words,
as well. In other words,  is in the closure
is in the closureClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
of V.
Using this relation we see that for
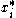 itself
itself  . We also know that
. We also know that  , so
, so  as well. Combining these we find that
as well. Combining these we find that  . We can use this equation to show that
. We can use this equation to show that  fits the definition of a price quasi-equilibrium with transfers.
fits the definition of a price quasi-equilibrium with transfers.Because
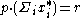 and
and 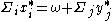 we know that for any firm j:
we know that for any firm j:-
 for
for 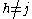
which implies
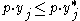 . Similarly we know:
. Similarly we know:-
 for
for 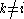
which implies
 . These two statements, along with the feasibility of the allocation at the Pareto optimum, satisfy the three conditions for a price quasi-equilibrium with transfers supported by wealth levels
. These two statements, along with the feasibility of the allocation at the Pareto optimum, satisfy the three conditions for a price quasi-equilibrium with transfers supported by wealth levels  for all i.
for all i.We now turn to conditions under which a price quasi-equilibrium is also a price equilibrium, in other words, conditions under which the statement "if
 then
then  " imples "if
" imples "if  then
then  ". For this to be true we need now to assume that the consumption set
". For this to be true we need now to assume that the consumption set  is convex and the preference relation
is convex and the preference relation  is continuous
is continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Then, if there exists a consumption vector
 such that
such that 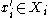 and
and  , a price quasi-equilibrium is a price equilibrium.
, a price quasi-equilibrium is a price equilibrium.To see why, assume to the contrary
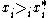 and
and 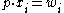 , and
, and  exists. Then by the convexity of
exists. Then by the convexity of  we have a bundle
we have a bundle 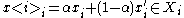 with
with  . By the continuity of
. By the continuity of  for
for  close to 1 we have
close to 1 we have  . This is a contradiction, because this bundle is preferred to
. This is a contradiction, because this bundle is preferred to  and costs less than
and costs less than  .
.Hence, for price quasi-equilibria to be price equilibria it is sufficient that the consumption set be convex, the preference relation to be continuous, and for there always to exist a "cheaper" consumption bundle
 . One way to ensure the existence of such a bundle is to require wealth levels
. One way to ensure the existence of such a bundle is to require wealth levels  to be strictly positive for all consumers i.
to be strictly positive for all consumers i.

