
Fulton-Hansen connectedness theorem
Encyclopedia
In mathematics
, the Fulton–Hansen connectedness theorem is a result from intersection theory
in algebraic geometry
, for the case of subvarieties of projective space
with codimension
large enough to make the intersection have components of dimension at least 1.
The formal statement is that if V and W are irreducible algebraic subvarieties of a projective space
P, all over an algebraically closed field
, and if
in terms of the dimension of an algebraic variety
, then the intersection U of V and W is connected
.
More generally, the theorem states that if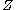 is a projective variety and
is a projective variety and 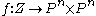 is any morphism such that
is any morphism such that 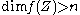 , then
, then 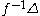 is connected, where
is connected, where  is the diagonal
is the diagonal
in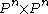 . The special case of intersections is recovered by taking
. The special case of intersections is recovered by taking  , with
, with 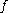 the natural inclusion.
the natural inclusion.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fulton–Hansen connectedness theorem is a result from intersection theory
Intersection theory
In mathematics, intersection theory is a branch of algebraic geometry, where subvarieties are intersected on an algebraic variety, and of algebraic topology, where intersections are computed within the cohomology ring. The theory for varieties is older, with roots in Bézout's theorem on curves and...
in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, for the case of subvarieties of projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
with codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
large enough to make the intersection have components of dimension at least 1.
The formal statement is that if V and W are irreducible algebraic subvarieties of a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
P, all over an algebraically closed field
Algebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, and if
- dim(V) + dim (W) > dim (P)
in terms of the dimension of an algebraic variety
Dimension of an algebraic variety
In mathematics, the dimension of an algebraic variety V in algebraic geometry is defined, informally speaking, as the number of independent rational functions that exist on V.For example, an algebraic curve has by definition dimension 1...
, then the intersection U of V and W is connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
.
More generally, the theorem states that if
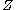 is a projective variety and
is a projective variety and 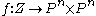 is any morphism such that
is any morphism such that 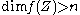 , then
, then 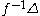 is connected, where
is connected, where  is the diagonal
is the diagonalDiagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
in
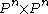 . The special case of intersections is recovered by taking
. The special case of intersections is recovered by taking  , with
, with 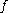 the natural inclusion.
the natural inclusion.See also
- Zariski's connectedness theorem
- Grothendieck's connectedness theoremGrothendieck's connectedness theoremIn mathematics, Grothendieck's connectedness theorem states thatif A is a complete local ring whose spectrum is k-connected and f is in the maximal ideal, then Spec is -connected...
- Deligne's connectedness theorem

