Free entropy
Encyclopedia
A thermodynamic free entropy is an entropic thermodynamic potential analogous to the free energy
. Also known as a Massieu, Planck, or Massieu-Planck potentials (or functions), or (rarely) free information. In statistical mechanics, free entropies frequently appear as the logarithm of a partition function
. In mathematics
, free entropy is the generalization of entropy defined in free probability
.
A free entropy is generated by a Legendre transform of the entropy. The different potentials correspond to different constraints to which the system may be subjected.
where
Note that the use of the terms "Massieu" and "Planck" for explicit Massieu-Planck potentials are somewhat obscure and ambiguous. In particular "Planck potential" has alternative meanings. The most standard notation for an entropic potential is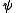
, used by both Planck and Schrödinger. (Note that Gibbs used 
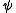to denote the free energy.) Free entropies where invented by French engineer Francois Massieu
in 1869, and actually predate Gibb's free energy (1875).
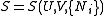
By the definition of a total differential,
.
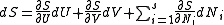From the equations of state,
.
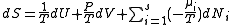The differentials in the above equation are all of extensive variables
, so they may be integrated to yield
.
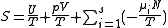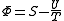
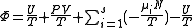
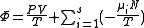
Starting over at the definition of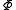
and taking the total differential, we have via a Legendre transform (and the chain rule
)
,
,
.
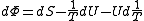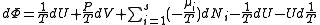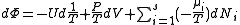The above differentials are not all of extensive variables, so the equation may not be directly integrated. From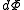
we see that
.
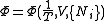If reciprocal variables are not desired,
,
,
,
,
.
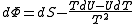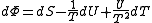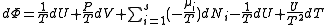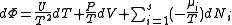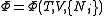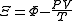
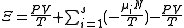
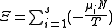
Starting over at the definition of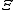
and taking the total differential, we have via a Legendre transform (and the chain rule
)
.
The above differentials are not all of extensive variables, so the equation may not be directly integrated. From
we see that
.
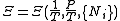If reciprocal variables are not desired,
,
,
,
,
.
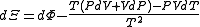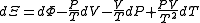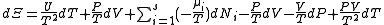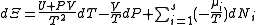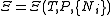Thermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
. Also known as a Massieu, Planck, or Massieu-Planck potentials (or functions), or (rarely) free information. In statistical mechanics, free entropies frequently appear as the logarithm of a partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
. In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, free entropy is the generalization of entropy defined in free probability
Free probability
Free probability is a mathematical theory that studies non-commutative random variables. The "freeness" or free independence property is the analogue of the classical notion of independence, and it is connected with free products....
.
A free entropy is generated by a Legendre transform of the entropy. The different potentials correspond to different constraints to which the system may be subjected.
Examples
The most common examples are:| Name | Function | Alt. function | Natural variables |
| Entropy Entropy Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when... |
 |
 |
|
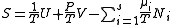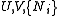| Massieu potential \ Helmholtz free entropy |  |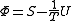
 |
 |
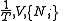| Planck potential \ Gibbs free entropy |  |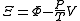
 |
 |
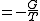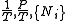where
-
is entropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...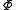
is the Massieu potential
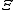is the Planck potential
is internal energyInternal energyIn thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
-
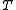is temperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
is pressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...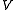
is volume
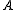is Helmholtz free energyHelmholtz free energyIn thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
-
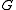is Gibbs free energyGibbs free energyIn thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
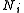is number of particlesParticle numberThe particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
(or number of moles) composing the i-th chemical component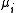
is the chemical potentialChemical potentialChemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
of the i-th chemical componentChemical speciesChemical species are atoms, molecules, molecular fragments, ions, etc., being subjected to a chemical process or to a measurement. Generally, a chemical species can be defined as an ensemble of chemically identical molecular entities that can explore the same set of molecular energy levels on a...
is the total number of componentsChemical speciesChemical species are atoms, molecules, molecular fragments, ions, etc., being subjected to a chemical process or to a measurement. Generally, a chemical species can be defined as an ensemble of chemically identical molecular entities that can explore the same set of molecular energy levels on a...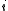
is the 
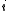th components.
Note that the use of the terms "Massieu" and "Planck" for explicit Massieu-Planck potentials are somewhat obscure and ambiguous. In particular "Planck potential" has alternative meanings. The most standard notation for an entropic potential is
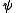, used by both Planck and Schrödinger. (Note that Gibbs used 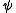to denote the free energy.) Free entropies where invented by French engineer Francois MassieuFrancois Massieu
In thermodynamics, Francois Jacques Dominique Massieu was a French engineer noted for his two 1869 characteristic functions, each of which known as a Massieu function , as cited by American engineer Willard Gibbs in his 1876 On the Equilibrium of Heterogeneous Substances.-External links:*Nivoit, E....
in 1869, and actually predate Gibb's free energy (1875).
Entropy
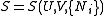
By the definition of a total differential,
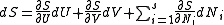.From the equations of state,
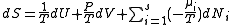.The differentials in the above equation are all of extensive variables
Intensive and extensive properties
In the physical sciences, an intensive property , is a physical property of a system that does not depend on the system size or the amount of material in the system: it is scale invariant.By contrast, an extensive property In the physical sciences, an intensive property (also called a bulk...
, so they may be integrated to yield
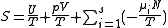.Massieu potential / Helmholtz free entropy
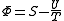
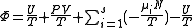
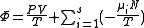
Starting over at the definition of
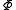and taking the total differential, we have via a Legendre transform (and the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
)
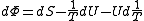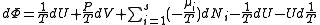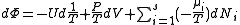,,.The above differentials are not all of extensive variables, so the equation may not be directly integrated. From
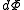we see that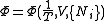.If reciprocal variables are not desired,
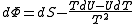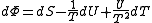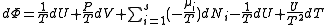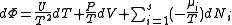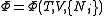,,,,.Planck potential / Gibbs free entropy
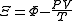
Starting over at the definition of
and taking the total differential, we have via a Legendre transform (and the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
)
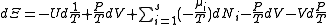
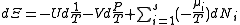.The above differentials are not all of extensive variables, so the equation may not be directly integrated. From
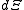we see that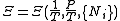.If reciprocal variables are not desired,
,,,,.
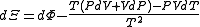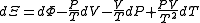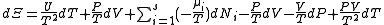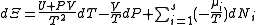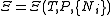