
Fourier amplitude sensitivity testing
Encyclopedia
Fourier amplitude sensitivity testing (FAST) is a variance-based global sensitivity analysis
method. The sensitivity value is defined based on conditional variance
s which indicate the individual or joint effects of the uncertain inputs on the output.
FAST first represents conditional variances via coefficients from the multiple Fourier series
expansion of the output function. Then the ergodic theorem is applied to transform the multi-dimensional integral to a one-dimensional integral in evaluation of the Fourier coefficients. A set of incommensurate frequencies is required to perform the transform and most frequencies are irrational. To facilitate computation a set of integer frequencies is selected instead of the irrational frequencies. The integer frequencies are not strictly incommensurate, resulting in an error between the multi-dimensional integral and the transformed one-dimensional integral. However, the integer frequencies can be selected to be incommensurate to any order so that the error can be controlled meeting any precision requirement in theory. Using integer frequencies in the integral transform, the resulted function in the one-dimensional integral is periodic and the integral only needs to evaluate in a single period. Next, since the continuous integral function can be recovered from a set of finite sampling points if the Nyquist–Shannon sampling theorem
is satisfied, the one-dimensional integral is evaluated from the summation of function values at the generated sampling points.
FAST is more efficient to calculate sensitivities than other variance-based global sensitivity analysis methods via Monte Carlo integration. However the calculation by FAST is usually limited to sensitivities referring to “main effect” or “total effect”.
computer program capable of analyzing either algebraic or differential equation systems was published in 1982. In 1990s, the relationship between FAST sensitivity indices and Sobol’s ones calculated from Monte-Carlo simulation was revealed in the general framework of ANOVA-like decomposition and an extended FAST method able to calculate sensitivity indices referring to “total effect” was developed.
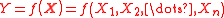 where
where 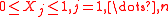 . The ANOVA-like decomposition is
. The ANOVA-like decomposition is
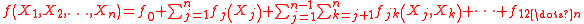
provided that is a constant and the integral of each term in the sums is zero, i.e.
is a constant and the integral of each term in the sums is zero, i.e.

The conditional variance which characterizes the contribution of each term to the total variance of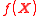 is
is
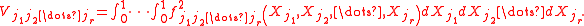
The total variance is the sum of all conditional variances

The sensitivity index is defined as the normalized conditional variance as

especially the first order sensitivity
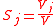
which indicates the main effect of the input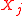 .
.
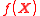 in the unit hyper-cube can be extended to a multiply periodic function and the multiple Fourier series expansion is
in the unit hyper-cube can be extended to a multiply periodic function and the multiple Fourier series expansion is
where the Fourier coefficient is
The ANOVA-like decomposition is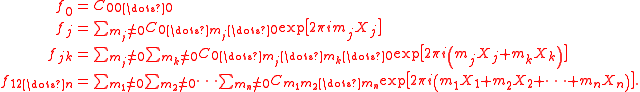
The first order conditional variance is
where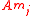 and
and 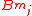 are the real and imaginary part of
are the real and imaginary part of  respectively
respectively
 as
as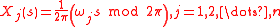
where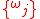 is a set of incommensurate frequencies, i.e.
is a set of incommensurate frequencies, i.e.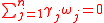
for an integer set of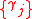 if and only if
if and only if 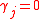 for every
for every 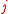 .
.
Then the Fourier coefficients can be calculated by a one-dimensional integral according to the ergodic theorem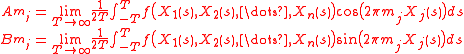
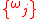 can be rational with all others being irrational. Since the numerical value of an irrational number cannot be stored exactly in a computer, an approximation of the incommensurate frequencies by all rational numbers is required in implementation. Without loss of any generality the frequencies can be set as integers instead of any rational numbers. A set of integers
can be rational with all others being irrational. Since the numerical value of an irrational number cannot be stored exactly in a computer, an approximation of the incommensurate frequencies by all rational numbers is required in implementation. Without loss of any generality the frequencies can be set as integers instead of any rational numbers. A set of integers 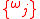 is approximately incommensurate to the order of
is approximately incommensurate to the order of  if
if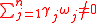
for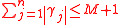
where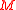 is an integer. The exact incommensurate condition is a extreme case when
is an integer. The exact incommensurate condition is a extreme case when  .
.
Using the integer frequencies the function in the transformed one-dimensional integral is periodic so only the integration over a period of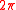 is required. The Fourier coefficients can be approximately calculated as
is required. The Fourier coefficients can be approximately calculated as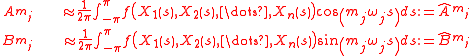
The approximation of the incommensurate frequencies for a finite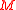 results in a discrepancy error between the true Fourier coefficients
results in a discrepancy error between the true Fourier coefficients 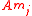 ,
, 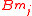 and their estimates
and their estimates 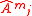 ,
, 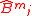 . The larger the order
. The larger the order 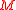 is the smaller the error is but the more computational efforts are required to calculate the estimates in the following procedure. In practice
is the smaller the error is but the more computational efforts are required to calculate the estimates in the following procedure. In practice 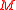 is frequently set to 4 and a table of resulted frequency sets which have up to 50 frequencies is available. (McRae et al., 1982)
is frequently set to 4 and a table of resulted frequency sets which have up to 50 frequencies is available. (McRae et al., 1982)
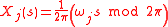 , defines a search curve in the input space. If the frequencies,
, defines a search curve in the input space. If the frequencies, 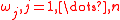 , are incommensurate, the search curve can pass through every point in the input space as
, are incommensurate, the search curve can pass through every point in the input space as  varies from 0 to
varies from 0 to  so the multi-dimensional integral over the input space can be accurately transformed to a one-dimensional integral along the search curve. However, if the frequencies are approximately incommensurate integers, the search curve cannot pass through every point in the input space. If fact the search is repeated since the transform function is periodic, with a period of
so the multi-dimensional integral over the input space can be accurately transformed to a one-dimensional integral along the search curve. However, if the frequencies are approximately incommensurate integers, the search curve cannot pass through every point in the input space. If fact the search is repeated since the transform function is periodic, with a period of 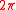 . The one-dimensional integratal can be evaluated over a single period instead of the infinite interval for incommensurate frequencies; However, a compuatational error arises due to the approximation of the incommensuracy.
. The one-dimensional integratal can be evaluated over a single period instead of the infinite interval for incommensurate frequencies; However, a compuatational error arises due to the approximation of the incommensuracy.

and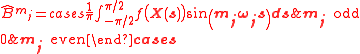
The non-zero integrals can be calculated from sampling points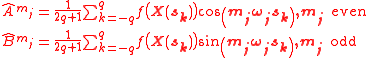
where the uniform sampling point in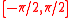 is
is
The total number of sampling points is which should satisfy the Nyquist sampling criterion, i.e.
which should satisfy the Nyquist sampling criterion, i.e.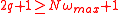
where is the largest frequency in
is the largest frequency in 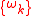 and
and  is the maximum order of the calculated Fourier coefficients.
is the maximum order of the calculated Fourier coefficients.
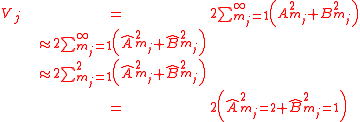
where only the partial sum of the first two terms is calculated and for determining the number of sampling points. Using the partial sum can usually return an adequately good approximation of the total sum since the terms corresponding to the fundamental frequency and low order frequencies usually contribute most to the total sum. Additionally, the Fourier coefficient in the summation are just an estimate of the true value and adding more higher order terms will not help improve the computational accuracy significantly. Sine the integer frequencies are not exactly incommensurate there are two integers
for determining the number of sampling points. Using the partial sum can usually return an adequately good approximation of the total sum since the terms corresponding to the fundamental frequency and low order frequencies usually contribute most to the total sum. Additionally, the Fourier coefficient in the summation are just an estimate of the true value and adding more higher order terms will not help improve the computational accuracy significantly. Sine the integer frequencies are not exactly incommensurate there are two integers  and
and 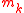 such that
such that 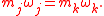 Interference between the two frequencies can occur if higher order terms are included in the summation.
Interference between the two frequencies can occur if higher order terms are included in the summation.
Similarly the total variance of can be calculated as
can be calculated as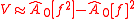
where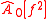 denotes the estimated Fourier coefficient of the function of
denotes the estimated Fourier coefficient of the function of 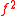 inside the bracket and
inside the bracket and 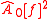 is the squared Fourier coefficient of the function
is the squared Fourier coefficient of the function 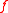 . Finally the sensitivity referring to the main effect of an input can be calculated by dividing the conditional variance by the total variance.
. Finally the sensitivity referring to the main effect of an input can be calculated by dividing the conditional variance by the total variance.
Sensitivity analysis
Sensitivity analysis is the study of how the variation in the output of a statistical model can be attributed to different variations in the inputs of the model. Put another way, it is a technique for systematically changing variables in a model to determine the effects of such changes.In any...
method. The sensitivity value is defined based on conditional variance
Conditional variance
In probability theory and statistics, a conditional variance is the variance of a conditional probability distribution. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function...
s which indicate the individual or joint effects of the uncertain inputs on the output.
FAST first represents conditional variances via coefficients from the multiple Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
expansion of the output function. Then the ergodic theorem is applied to transform the multi-dimensional integral to a one-dimensional integral in evaluation of the Fourier coefficients. A set of incommensurate frequencies is required to perform the transform and most frequencies are irrational. To facilitate computation a set of integer frequencies is selected instead of the irrational frequencies. The integer frequencies are not strictly incommensurate, resulting in an error between the multi-dimensional integral and the transformed one-dimensional integral. However, the integer frequencies can be selected to be incommensurate to any order so that the error can be controlled meeting any precision requirement in theory. Using integer frequencies in the integral transform, the resulted function in the one-dimensional integral is periodic and the integral only needs to evaluate in a single period. Next, since the continuous integral function can be recovered from a set of finite sampling points if the Nyquist–Shannon sampling theorem
Nyquist–Shannon sampling theorem
The Nyquist–Shannon sampling theorem, after Harry Nyquist and Claude Shannon, is a fundamental result in the field of information theory, in particular telecommunications and signal processing. Sampling is the process of converting a signal into a numeric sequence...
is satisfied, the one-dimensional integral is evaluated from the summation of function values at the generated sampling points.
FAST is more efficient to calculate sensitivities than other variance-based global sensitivity analysis methods via Monte Carlo integration. However the calculation by FAST is usually limited to sensitivities referring to “main effect” or “total effect”.
History
The FAST method originated in study of coupled chemical reaction systems in 1973 and the detailed analysis of the computational error was presented latter in 1975. Only the first order sensitivity indices referring to “main effect” were calculated in the original method. A FORTRANFortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
computer program capable of analyzing either algebraic or differential equation systems was published in 1982. In 1990s, the relationship between FAST sensitivity indices and Sobol’s ones calculated from Monte-Carlo simulation was revealed in the general framework of ANOVA-like decomposition and an extended FAST method able to calculate sensitivity indices referring to “total effect” was developed.
Variance-based sensitivity
Sensitivity indices of a variance-based method are calculated via ANOVA-like decomposition of the function for analysis. Suppose the function is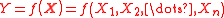 where
where 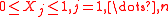 . The ANOVA-like decomposition is
. The ANOVA-like decomposition is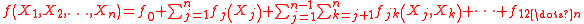
provided that
 is a constant and the integral of each term in the sums is zero, i.e.
is a constant and the integral of each term in the sums is zero, i.e.
The conditional variance which characterizes the contribution of each term to the total variance of
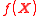 is
is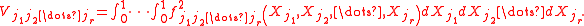
The total variance is the sum of all conditional variances

The sensitivity index is defined as the normalized conditional variance as

especially the first order sensitivity
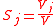
which indicates the main effect of the input
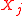 .
.Multiple Fourier series
One way to calculate the ANOVA-like decomposition is based on multiple Fourier series. The function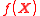 in the unit hyper-cube can be extended to a multiply periodic function and the multiple Fourier series expansion is
in the unit hyper-cube can be extended to a multiply periodic function and the multiple Fourier series expansion is
where the Fourier coefficient is

The ANOVA-like decomposition is
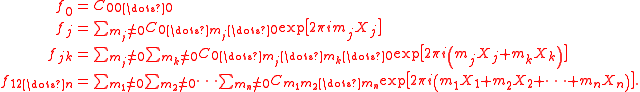
The first order conditional variance is

where
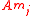 and
and 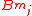 are the real and imaginary part of
are the real and imaginary part of  respectively
respectively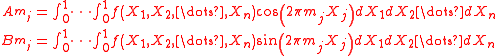
Ergodic theorem
A multi-dimensional integral is required to evaluate for calculating the Fourier coefficients. One way is to transform the multi-dimensional integral into a one-dimensional integral by expressing every input as a function of a new independent variable as
as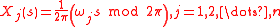
where
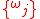 is a set of incommensurate frequencies, i.e.
is a set of incommensurate frequencies, i.e.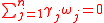
for an integer set of
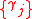 if and only if
if and only if 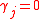 for every
for every 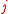 .
.Then the Fourier coefficients can be calculated by a one-dimensional integral according to the ergodic theorem
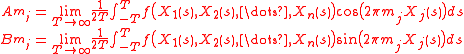
Integer frequencies
At most one of the incommensurate frequencies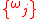 can be rational with all others being irrational. Since the numerical value of an irrational number cannot be stored exactly in a computer, an approximation of the incommensurate frequencies by all rational numbers is required in implementation. Without loss of any generality the frequencies can be set as integers instead of any rational numbers. A set of integers
can be rational with all others being irrational. Since the numerical value of an irrational number cannot be stored exactly in a computer, an approximation of the incommensurate frequencies by all rational numbers is required in implementation. Without loss of any generality the frequencies can be set as integers instead of any rational numbers. A set of integers 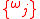 is approximately incommensurate to the order of
is approximately incommensurate to the order of  if
if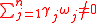
for
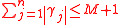
where
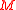 is an integer. The exact incommensurate condition is a extreme case when
is an integer. The exact incommensurate condition is a extreme case when  .
.Using the integer frequencies the function in the transformed one-dimensional integral is periodic so only the integration over a period of
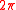 is required. The Fourier coefficients can be approximately calculated as
is required. The Fourier coefficients can be approximately calculated as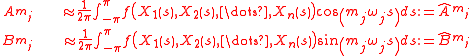
The approximation of the incommensurate frequencies for a finite
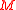 results in a discrepancy error between the true Fourier coefficients
results in a discrepancy error between the true Fourier coefficients 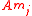 ,
, 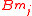 and their estimates
and their estimates 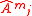 ,
, 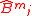 . The larger the order
. The larger the order 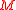 is the smaller the error is but the more computational efforts are required to calculate the estimates in the following procedure. In practice
is the smaller the error is but the more computational efforts are required to calculate the estimates in the following procedure. In practice 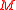 is frequently set to 4 and a table of resulted frequency sets which have up to 50 frequencies is available. (McRae et al., 1982)
is frequently set to 4 and a table of resulted frequency sets which have up to 50 frequencies is available. (McRae et al., 1982)Search curve
The transform,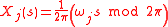 , defines a search curve in the input space. If the frequencies,
, defines a search curve in the input space. If the frequencies, 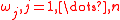 , are incommensurate, the search curve can pass through every point in the input space as
, are incommensurate, the search curve can pass through every point in the input space as  varies from 0 to
varies from 0 to  so the multi-dimensional integral over the input space can be accurately transformed to a one-dimensional integral along the search curve. However, if the frequencies are approximately incommensurate integers, the search curve cannot pass through every point in the input space. If fact the search is repeated since the transform function is periodic, with a period of
so the multi-dimensional integral over the input space can be accurately transformed to a one-dimensional integral along the search curve. However, if the frequencies are approximately incommensurate integers, the search curve cannot pass through every point in the input space. If fact the search is repeated since the transform function is periodic, with a period of 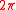 . The one-dimensional integratal can be evaluated over a single period instead of the infinite interval for incommensurate frequencies; However, a compuatational error arises due to the approximation of the incommensuracy.
. The one-dimensional integratal can be evaluated over a single period instead of the infinite interval for incommensurate frequencies; However, a compuatational error arises due to the approximation of the incommensuracy.Sampling
The approximated Fourier can be further expressed as
and
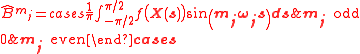
The non-zero integrals can be calculated from sampling points
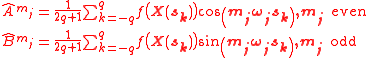
where the uniform sampling point in
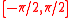 is
is
The total number of sampling points is
 which should satisfy the Nyquist sampling criterion, i.e.
which should satisfy the Nyquist sampling criterion, i.e.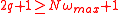
where
 is the largest frequency in
is the largest frequency in 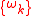 and
and  is the maximum order of the calculated Fourier coefficients.
is the maximum order of the calculated Fourier coefficients.Partial sum
After calculating the estimated Fourier coefficients, the first order conditional variance can be approximated by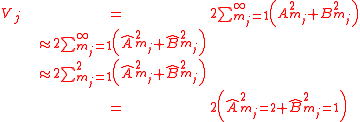
where only the partial sum of the first two terms is calculated and
 for determining the number of sampling points. Using the partial sum can usually return an adequately good approximation of the total sum since the terms corresponding to the fundamental frequency and low order frequencies usually contribute most to the total sum. Additionally, the Fourier coefficient in the summation are just an estimate of the true value and adding more higher order terms will not help improve the computational accuracy significantly. Sine the integer frequencies are not exactly incommensurate there are two integers
for determining the number of sampling points. Using the partial sum can usually return an adequately good approximation of the total sum since the terms corresponding to the fundamental frequency and low order frequencies usually contribute most to the total sum. Additionally, the Fourier coefficient in the summation are just an estimate of the true value and adding more higher order terms will not help improve the computational accuracy significantly. Sine the integer frequencies are not exactly incommensurate there are two integers  and
and 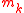 such that
such that 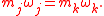 Interference between the two frequencies can occur if higher order terms are included in the summation.
Interference between the two frequencies can occur if higher order terms are included in the summation.Similarly the total variance of
 can be calculated as
can be calculated as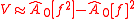
where
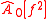 denotes the estimated Fourier coefficient of the function of
denotes the estimated Fourier coefficient of the function of 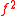 inside the bracket and
inside the bracket and 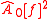 is the squared Fourier coefficient of the function
is the squared Fourier coefficient of the function 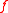 . Finally the sensitivity referring to the main effect of an input can be calculated by dividing the conditional variance by the total variance.
. Finally the sensitivity referring to the main effect of an input can be calculated by dividing the conditional variance by the total variance.

