Formal calculation
Encyclopedia
In mathematical logic
, a formal calculation is sometimes defined as a calculation which is systematic, but without a rigorous justification. This means that we are manipulating the symbols in an expression using a generic substitution, without proving that the necessary conditions hold. Essentially, we are interested in the form of an expression, and not necessarily its underlying meaning. This reasoning can either serve as positive evidence that some statement is true, when it is difficult or unnecessary to provide a proof, or as an inspiration for the creation of new (completely rigorous) definitions.
However, this interpretation of the term formal is not universally accepted, and some consider it to mean quite the opposite: A completely rigorous argument, as in formal mathematical logic
.
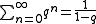
(which holds under certain conditions) to conclude that
This is incorrect according to the usual definition of infinite sums of real numbers, since the related sequence does not converge. However, this result can inspire extending the definition of infinite sums, and the creation of new fields, such as the 2-adic numbers
, where the series in question converges and this statement is perfectly valid.
is a concept that adopts some properties of convergent power series used in real analysis
, and applies them to objects that are similar to power series in form, but have nothing to do with the notion of convergence.
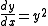
Treating these symbols as ordinary algebraic ones, and without giving any justification regarding the validity of this step, we take reciprocals of both sides:
Now we take a simple antiderivative
:
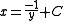
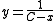
Because this is a formal calculation, we can also allow ourselves to let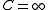
and obtain another solution:
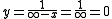
If we have any doubts about our argument, we can always check the final solutions to confirm that they solve the equation.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a formal calculation is sometimes defined as a calculation which is systematic, but without a rigorous justification. This means that we are manipulating the symbols in an expression using a generic substitution, without proving that the necessary conditions hold. Essentially, we are interested in the form of an expression, and not necessarily its underlying meaning. This reasoning can either serve as positive evidence that some statement is true, when it is difficult or unnecessary to provide a proof, or as an inspiration for the creation of new (completely rigorous) definitions.
However, this interpretation of the term formal is not universally accepted, and some consider it to mean quite the opposite: A completely rigorous argument, as in formal mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
.
A simple example
A somewhat exaggerated example would be to use the equation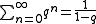(which holds under certain conditions) to conclude that
This is incorrect according to the usual definition of infinite sums of real numbers, since the related sequence does not converge. However, this result can inspire extending the definition of infinite sums, and the creation of new fields, such as the 2-adic numbers
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
, where the series in question converges and this statement is perfectly valid.
Formal power series
Formal power seriesFormal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
is a concept that adopts some properties of convergent power series used in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, and applies them to objects that are similar to power series in form, but have nothing to do with the notion of convergence.
Symbol manipulation
Suppose we want to solve the differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
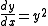
Treating these symbols as ordinary algebraic ones, and without giving any justification regarding the validity of this step, we take reciprocals of both sides:
Now we take a simple antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
:
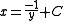
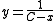
Because this is a formal calculation, we can also allow ourselves to let
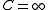and obtain another solution: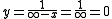If we have any doubts about our argument, we can always check the final solutions to confirm that they solve the equation.