
First-order reduction
Encyclopedia
A first-order reduction is a very weak type of reduction
between two computational problem
s in computational complexity theory
. A first-order reduction is a reduction where each component is restricted to be in the class FO
of problems calculable in first-order logic
.
Since we have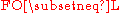 , the first-order reductions are weaker reductions than the logspace reductions.
, the first-order reductions are weaker reductions than the logspace reductions.
Many important complexity classes are closed under first-order reductions, and many of the traditional complete
problems are first-order complete as well (Immerman 1999 p. 49-50). For example, ST-connectivity
is FO-complete for NL
, and NL
is closed under FO reductions (Immerman 1999, p. 51) (as are P
, NP
, and most other "well-behaved" classes).
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
between two computational problem
Computational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
s in computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
. A first-order reduction is a reduction where each component is restricted to be in the class FO
FO (complexity)
FO is the complexity class of structures which can be recognised by formulae of first-order logic. It is the foundation of the field of descriptive complexity and is equal to the complexity class AC0 FO-regular...
of problems calculable in first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
.
Since we have
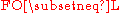 , the first-order reductions are weaker reductions than the logspace reductions.
, the first-order reductions are weaker reductions than the logspace reductions.Many important complexity classes are closed under first-order reductions, and many of the traditional complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
problems are first-order complete as well (Immerman 1999 p. 49-50). For example, ST-connectivity
ST-connectivity
In computer science and computational complexity theory, st-connectivity or STCON is a decision problem asking, for vertices s and t in a directed graph, if t is reachable from s.Formally, the decision problem is given by- Complexity :...
is FO-complete for NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
, and NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
is closed under FO reductions (Immerman 1999, p. 51) (as are P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, and most other "well-behaved" classes).

