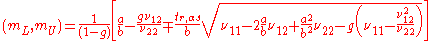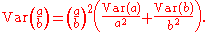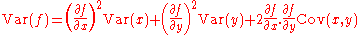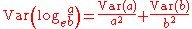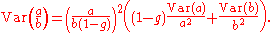Fieller's theorem
Encyclopedia
In statistics
, Fieller's theorem allows the calculation of a confidence interval
for the ratio of two means
.
s as they may also be in different units. The most complete discussion of this is given by Fieller (1954).
Fieller showed that if a and b are (possibly correlated
) means of two samples with expectations
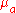 and
and 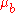 , and variances
, and variances 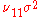 and
and 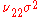 and covariance
and covariance 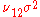 , and if
, and if 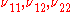 are all known, then a (1 − α) confidence interval (mL, mU) for
are all known, then a (1 − α) confidence interval (mL, mU) for 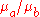 is given by
is given by
where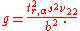
Here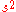 is an unbiased estimator
is an unbiased estimator
of based on r degrees of freedom, and
based on r degrees of freedom, and 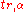 is the
is the  -level deviate from the Student's t-distribution based on r degrees of freedom.
-level deviate from the Student's t-distribution based on r degrees of freedom.
Three features of this formula are important in this context:
a) The expression inside the square root has to be positive, or else the resulting interval will be imaginary.
b) When g is very close to 1, the confidence interval is infinite.
c) When g is greater than 1, the overall divisor outside the square brackets is negative and the confidence interval is exclusive.
From this a 95% confidence interval can be constructed in the usual way (degrees of freedom for t * is equal to the total number of values in the numerator and denominator minus 2).
This can be expressed in a more useful form for when (as is usually the case) logged data is used, using the following relation for a function of x and y, say ƒ(x, y):
to obtain either,
or
First, calculate the intermediate quantity:
You cannot calculate the confidence interval of the quotient if , as the CI for the denominator μb will include zero.
, as the CI for the denominator μb will include zero.
However if then we can obtain
then we can obtain
provides another alternative that that does not require the assumption of normality.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Fieller's theorem allows the calculation of a confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
for the ratio of two means
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
.
Approximate confidence interval
Variables a and b may be measured in different units, so there is no way to directly combine the standard errorStandard error
Standard error can refer to:* Standard error , the estimated standard deviation or error of a series of measurements* Standard error stream, one of the standard streams in Unix-like operating systems...
s as they may also be in different units. The most complete discussion of this is given by Fieller (1954).
Fieller showed that if a and b are (possibly correlated
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
) means of two samples with expectations
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
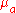 and
and 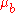 , and variances
, and variances 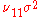 and
and 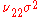 and covariance
and covariance 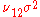 , and if
, and if 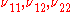 are all known, then a (1 − α) confidence interval (mL, mU) for
are all known, then a (1 − α) confidence interval (mL, mU) for 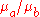 is given by
is given bywhere
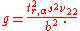
Here
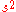 is an unbiased estimator
is an unbiased estimatorBias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
of
 based on r degrees of freedom, and
based on r degrees of freedom, and 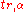 is the
is the  -level deviate from the Student's t-distribution based on r degrees of freedom.
-level deviate from the Student's t-distribution based on r degrees of freedom.Three features of this formula are important in this context:
a) The expression inside the square root has to be positive, or else the resulting interval will be imaginary.
b) When g is very close to 1, the confidence interval is infinite.
c) When g is greater than 1, the overall divisor outside the square brackets is negative and the confidence interval is exclusive.
Approximate formulae
These equations approximation to the full formula, and are obtained via a Taylor series expansion of a function of two variables and then taking the variance (i.e. a generalisation to two variables of the formula for the approximate standard error for a function of an estimate).Case 1
Assume that a and b are jointly normally distributed, and that b is not too near zero (i.e. more specifically, that the standard error of b is small compared to b),From this a 95% confidence interval can be constructed in the usual way (degrees of freedom for t * is equal to the total number of values in the numerator and denominator minus 2).
This can be expressed in a more useful form for when (as is usually the case) logged data is used, using the following relation for a function of x and y, say ƒ(x, y):
to obtain either,
or
Case 2
Assume that a and b are jointly normally distributed, and that b is near zero (i.e. SE(b) is not small compared to b).First, calculate the intermediate quantity:
You cannot calculate the confidence interval of the quotient if
 , as the CI for the denominator μb will include zero.
, as the CI for the denominator μb will include zero.However if
 then we can obtain
then we can obtainOther
One problem is that, when g is not small, CIs can blow up when using Fieller's theorem. Andy Grieve has provided a Bayesian solution where the CIs are still sensible, albeit wide. BootstrappingBootstrapping
Bootstrapping or booting refers to a group of metaphors that share a common meaning: a self-sustaining process that proceeds without external help....
provides another alternative that that does not require the assumption of normality.
History
Edgar C. Fieller (1907–1960) was a statistician employed in the pharmaceutical industry, specifically by Boots.Further reading
- Fieller, EC. (1932) "The distribution of the index in a bivariate Normal distribution". BiometrikaBiometrika- External links :* . The Internet Archive. 2011....
, 24(3–4):428–440. - Fieller, EC. (1940) "The biological standardisation of insulin". Journal of the Royal Statistical SocietyJournal of the Royal Statistical SocietyThe Journal of the Royal Statistical Society is a series of three peer-reviewed statistics journals published by Blackwell Publishing for the London-based Royal Statistical Society.- History :...
(Supplement). 1:1–54. - Fieller, EC. (1944) "A fundamental formula in the statistics of biological assay, and some applications". Quarterly Journal of Pharmacy and Pharmacology. 17: 117-123.
- Motulsky, Harvey (1995) Intuitive Biostatistics. Oxford University Press. ISBN 0-19-508607-4
- Senn, Steven (2007) Statistical Issues in Drug Development. Second Edition. Wiley. ISBN 0471974889