
Fermi coordinates
Encyclopedia
In the mathematical theory
of Riemannian geometry
, Fermi coordinates are local coordinates that are adapted to a geodesic
.
More formally, suppose M is an n-dimensional Riemannian manifold
,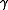 is a geodesic on
is a geodesic on 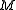 , and
, and 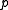 is a point on
is a point on 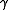 . Then there exists local coordinates
. Then there exists local coordinates 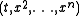
around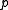 such that:
such that:
Such coordinates are called Fermi coordinates and are named after the Italian physicist Enrico Fermi
. The above properties are only valid on the geodesic. For example, if all Christoffel symbols vanish near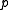 , then the manifold is flat near
, then the manifold is flat near  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, Fermi coordinates are local coordinates that are adapted to a geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
.
More formally, suppose M is an n-dimensional Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
,
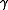 is a geodesic on
is a geodesic on 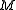 , and
, and 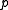 is a point on
is a point on 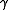 . Then there exists local coordinates
. Then there exists local coordinates 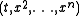
around
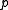 such that:
such that:
- For small t,
 represents the geodesic near
represents the geodesic near  ,
, - On
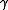 , the metric tensor is the Euclidean metric,
, the metric tensor is the Euclidean metric, - On
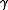 , all Christoffel symbols vanish.
, all Christoffel symbols vanish.
Such coordinates are called Fermi coordinates and are named after the Italian physicist Enrico Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
. The above properties are only valid on the geodesic. For example, if all Christoffel symbols vanish near
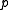 , then the manifold is flat near
, then the manifold is flat near  .
.See also
- Geodesic normal coordinates
- Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
- Isothermal coordinatesIsothermal coordinatesIn mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifoldare local coordinates where the metric isconformal to the Euclidean metric...

