Fermi's golden rule
Encyclopedia
In quantum physics, Fermi's golden rule is a way to calculate the transition rate (probability of transition per unit time) from one energy eigenstate of a quantum system into a continuum of energy eigenstates, due to a perturbation
.
We consider the system to begin in an eigenstate,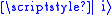
, of a given Hamiltonian
,
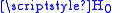. We consider the effect of a (possibly time-dependent) perturbing Hamiltonian, 
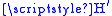. If 
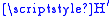is time-independent, the system goes only into those states in the continuum that have the same energy as the initial state. If 
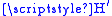is oscillating as a function of time with an angular frequency
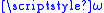, the transition is into states with energies that differ by 
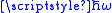from the energy of the initial state. In both cases, the one-to-many transition probability per unit of time from the state 
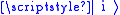to a set of final states 
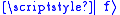is given, to first order in the perturbation, by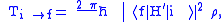
where
is the density of final states
(number of states per unit of energy) and
is the matrix element (in bra-ket notation
) of the perturbation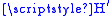
between the final and initial states.This transition probability is also called decay probability and is related to mean lifetime.
Fermi's golden rule is valid when the initial state has not been significantly depleted by scattering into the final states.
The most common way to derive the equation is to start with time-dependent perturbation theory and to take the limit for absorption under the assumption that the time of the measurement is much larger than the time needed for the transition.
Although named after Fermi
, most of the work leading to the Golden Rule was done by Dirac
who formulated an almost identical equation, including the three components of a constant, the matrix element of the perturbation and an energy difference. It is given its name because, being such a useful relation, Fermi himself called it "Golden Rule No. 2." It is thus an example of Stigler's Law.
Only the modulus of the matrix element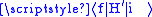
enters the Fermi's Golden Rule. The phase of this matrix element, however, contains separate information about the transition process.
It appears in expressions that complement the Golden Rule in the semiclassical Boltzmann equation approach to electron transport.
Perturbation theory (quantum mechanics)
In quantum mechanics, perturbation theory is a set of approximation schemes directly related to mathematical perturbation for describing a complicated quantum system in terms of a simpler one. The idea is to start with a simple system for which a mathematical solution is known, and add an...
.
We consider the system to begin in an eigenstate,
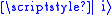, of a given HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
,
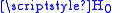. We consider the effect of a (possibly time-dependent) perturbing Hamiltonian, 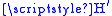. If 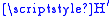is time-independent, the system goes only into those states in the continuum that have the same energy as the initial state. If 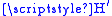is oscillating as a function of time with an angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
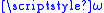, the transition is into states with energies that differ by 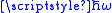from the energy of the initial state. In both cases, the one-to-many transition probability per unit of time from the state 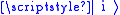to a set of final states 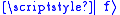is given, to first order in the perturbation, by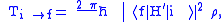where
is the density of final statesDensity of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...
(number of states per unit of energy) and
is the matrix element (in bra-ket notationBra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
) of the perturbation
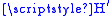between the final and initial states.This transition probability is also called decay probability and is related to mean lifetime.Fermi's golden rule is valid when the initial state has not been significantly depleted by scattering into the final states.
The most common way to derive the equation is to start with time-dependent perturbation theory and to take the limit for absorption under the assumption that the time of the measurement is much larger than the time needed for the transition.
Although named after Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
, most of the work leading to the Golden Rule was done by Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
who formulated an almost identical equation, including the three components of a constant, the matrix element of the perturbation and an energy difference. It is given its name because, being such a useful relation, Fermi himself called it "Golden Rule No. 2." It is thus an example of Stigler's Law.
Only the modulus of the matrix element
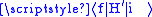enters the Fermi's Golden Rule. The phase of this matrix element, however, contains separate information about the transition process.It appears in expressions that complement the Golden Rule in the semiclassical Boltzmann equation approach to electron transport.