
Fermat–Catalan conjecture
Encyclopedia
In number theory
, the Fermat–Catalan conjecture combines ideas of Fermat's last theorem
and the Catalan conjecture, hence the name. The conjecture states that the equation
has only finitely many solutions (a,b,c,m,n,k); here a, b, c are positive coprime
integers and m, n, k are positive integers satisfying
As of 2008, the following solutions to are known:
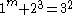
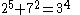
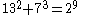
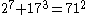
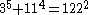
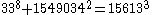
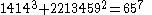
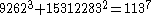
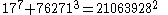
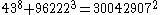
The first of these (1m+23=32) is the only solution where one of a, b or c is 1; this is the Catalan conjecture, proven in 2002 by Preda Mihăilescu
. Technically, this case leads infinitely many solutions of (since we can pick any m for m>6), but for the purposes of the statement of the Fermat-Catalan conjecture we count all these solutions as one.
It is known by Faltings' theorem
that for any fixed choice of positive integers m, n and k satisfying , only finitely many coprime triples (a, b, c) solving exist, but of course the full Fermat–Catalan conjecture is a much stronger statement.
The abc conjecture
implies the Fermat–Catalan conjecture.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Fermat–Catalan conjecture combines ideas of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
and the Catalan conjecture, hence the name. The conjecture states that the equation
has only finitely many solutions (a,b,c,m,n,k); here a, b, c are positive coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integers and m, n, k are positive integers satisfying
As of 2008, the following solutions to are known:
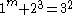
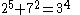
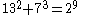
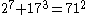
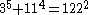
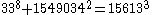
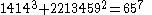
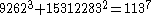
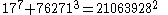
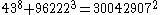
The first of these (1m+23=32) is the only solution where one of a, b or c is 1; this is the Catalan conjecture, proven in 2002 by Preda Mihăilescu
Preda Mihailescu
Preda V. Mihăilescu is a Romanian mathematician, best known for his proof of Catalan's conjecture.Born in Bucharest, he is the brother of Vintilă Mihăilescu. After leaving Romania in 1973, he settled in Switzerland. He studied mathematics and computer science in Zürich, receiving his Ph.D. from...
. Technically, this case leads infinitely many solutions of (since we can pick any m for m>6), but for the purposes of the statement of the Fermat-Catalan conjecture we count all these solutions as one.
It is known by Faltings' theorem
Faltings' theorem
In number theory, the Mordell conjecture is the conjecture made by that a curve of genus greater than 1 over the field Q of rational numbers has only finitely many rational points. The conjecture was later generalized by replacing Q by a finite extension...
that for any fixed choice of positive integers m, n and k satisfying , only finitely many coprime triples (a, b, c) solving exist, but of course the full Fermat–Catalan conjecture is a much stronger statement.
The abc conjecture
Abc conjecture
The abc conjecture is a conjecture in number theory, first proposed by Joseph Oesterlé and David Masser in 1985. The conjecture is stated in terms of three positive integers, a, b and c , which have no common factor and satisfy a + b = c...
implies the Fermat–Catalan conjecture.

