
Fall factor
Encyclopedia
In climbing
, (specifically in lead climbing
) using a dynamic rope
, the fall factor f is the ratio of the height h a climber falls before the climber's rope begins to stretch and the rope length L available to absorb the energy of the fall.
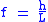
(HO) the impact force Fmax in the rope is given by:

where mg is the climber's weight, h is the fall height and k is the spring constant of the rope. Using the elasticity modulus E = k L/q which is a material constant, the impact force depends only on the fall factor f, i.e. on the ratio h/L, the cross section q of the rope and the climber’s weight. The more rope is available, the softer the rope becomes which is just compensating the higher fall energy. The maximum force on the climber is Fmax reduced by the climber’s weight mg. The above formula can be easily obtained by the law of conservation of energy at the time of maximum tension resp. maximum elongation xmax of the rope:
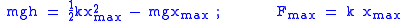
Using the HO model to obtain the impact force of real climbing ropes as a function of fall height h and climber's weight mg, one must know the experimental value for E of a given rope. However, rope manufacturers give only the rope’s impact force F0 and its static and dynamic elongations that are measured under standard UIAA fall conditions: A fall height h0 of 2 x 2.3m with an available rope length L0 = 2.6m leads to a fall factor f0 = h0/L0 = 1.77 and a fall velocity v0 = (2gh0)1/2 = 9.5m/sec at the end of falling the distance h0. The mass m0 used in the fall is 80kg. Using these values to eliminate the unknown quantity E leads to an expression of the impact force as a function of arbitrary fall heights h and arbitrary fall factors f of the form:

This simple undamped harmonic oscillator model of a rope, however, cannot explain real ropes. First, it is evident that real ropes hardly oscillate after a fall. After one period the rope has settled and stopped oscillating. The HO also cannot explain correctly the experimental values of a climbing rope such as its static and dynamic elongation and the correct relations to its impact force. This can be corrected only by considering friction in the rope. On the basis of a Viscoelastic Standard Linear Solid model one gets more complicated expressions for impact force and static and dynamic elongations. Friction in the rope leads to energy dissipation and thus to a reduction of the impact force compared to the undamped harmonic oscillator model. It also leads to an additional elongation of the rope. The diagram shows how the impact forces of real climbing ropes under standard UIAA fall conditions relate to their measured dynamic elongations. It also shows that the HO model cannot explain these dependencies of real climbing ropes.
When the rope is clipped into several carabiners between the climber and the belayer, an additional type of friction occurs, the so called dry friction
between the rope and particularly the last clipped carabiner. Dry friction leads to an effective rope length smaller than the available length L and thus increases the impact force. Dry friction is also responsible for the rope drag a climber has to overcome in order to move forward. It can be expressed by an effective mass of the rope that the climber has to pull which is always larger than the rope mass itself. It depends exponentially on the sum of the angles of the direction changes the climber has made.
fall, since the length of an arrested fall cannot exceed two times the length of the rope. Normally, a factor-2 fall can occur only when a lead climber who has placed no protection
falls past the belayer (two times the distance of the rope length between them), or the anchor if the climber is solo climbing the route using a self-belay. As soon as the climber clips the rope into protection above the belay, the distance of the potential fall as a function of rope length is lessened, and the fall factor drops below 2.
A fall of 20 feet is much more severe (exerts more force on the climber and climbing equipment) if it occurs with 10 feet of rope out (i.e. the climber has placed no protection and falls from 10 feet above the belayer to 10 feet below—a factor 2 fall) than if it occurs 100 feet above the belayer (a fall factor of 0.2), in which case the stretch of the rope more effectively cushions the fall.
, fall factors can be much higher. This is possible because the length of rope between harness and carabiner
is short and fixed, while the distance the climber can fall depends on the gaps between anchor points of the safety cable.
Climbing
Climbing is the activity of using one's hands and feet to ascend a steep object. It is done both for recreation and professionally, as part of activities such as maintenance of a structure, or military operations.Climbing activities include:* Bouldering: Ascending boulders or small...
, (specifically in lead climbing
Lead climbing
Lead climbing is a climbing technique used to ascend a route. This technique is predominantly used in rock climbing and involves a lead climber attaching themselves to a length of dynamic climbing rope and ascending a route while periodically attaching protection to the face of the route and...
) using a dynamic rope
Dynamic rope
A dynamic rope is a specially constructed, stretchable rope. This 'stretch' is what makes it 'dynamic', in contrast to a static rope that doesn't have any give when under load. By stretching under load, a dynamic rope will soften the impact of extreme stresses on it, such as falls, and lessens the...
, the fall factor f is the ratio of the height h a climber falls before the climber's rope begins to stretch and the rope length L available to absorb the energy of the fall.
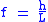
Impact force
The impact force is defined as the maximum tension in the rope when a climber falls. Using the common rope model of an undamped harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
(HO) the impact force Fmax in the rope is given by:

where mg is the climber's weight, h is the fall height and k is the spring constant of the rope. Using the elasticity modulus E = k L/q which is a material constant, the impact force depends only on the fall factor f, i.e. on the ratio h/L, the cross section q of the rope and the climber’s weight. The more rope is available, the softer the rope becomes which is just compensating the higher fall energy. The maximum force on the climber is Fmax reduced by the climber’s weight mg. The above formula can be easily obtained by the law of conservation of energy at the time of maximum tension resp. maximum elongation xmax of the rope:
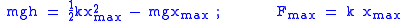
Using the HO model to obtain the impact force of real climbing ropes as a function of fall height h and climber's weight mg, one must know the experimental value for E of a given rope. However, rope manufacturers give only the rope’s impact force F0 and its static and dynamic elongations that are measured under standard UIAA fall conditions: A fall height h0 of 2 x 2.3m with an available rope length L0 = 2.6m leads to a fall factor f0 = h0/L0 = 1.77 and a fall velocity v0 = (2gh0)1/2 = 9.5m/sec at the end of falling the distance h0. The mass m0 used in the fall is 80kg. Using these values to eliminate the unknown quantity E leads to an expression of the impact force as a function of arbitrary fall heights h and arbitrary fall factors f of the form:

This simple undamped harmonic oscillator model of a rope, however, cannot explain real ropes. First, it is evident that real ropes hardly oscillate after a fall. After one period the rope has settled and stopped oscillating. The HO also cannot explain correctly the experimental values of a climbing rope such as its static and dynamic elongation and the correct relations to its impact force. This can be corrected only by considering friction in the rope. On the basis of a Viscoelastic Standard Linear Solid model one gets more complicated expressions for impact force and static and dynamic elongations. Friction in the rope leads to energy dissipation and thus to a reduction of the impact force compared to the undamped harmonic oscillator model. It also leads to an additional elongation of the rope. The diagram shows how the impact forces of real climbing ropes under standard UIAA fall conditions relate to their measured dynamic elongations. It also shows that the HO model cannot explain these dependencies of real climbing ropes.
When the rope is clipped into several carabiners between the climber and the belayer, an additional type of friction occurs, the so called dry friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
between the rope and particularly the last clipped carabiner. Dry friction leads to an effective rope length smaller than the available length L and thus increases the impact force. Dry friction is also responsible for the rope drag a climber has to overcome in order to move forward. It can be expressed by an effective mass of the rope that the climber has to pull which is always larger than the rope mass itself. It depends exponentially on the sum of the angles of the direction changes the climber has made.
Lead climbing
A fall factor of two is the maximum that is possible in a lead climbingLead climbing
Lead climbing is a climbing technique used to ascend a route. This technique is predominantly used in rock climbing and involves a lead climber attaching themselves to a length of dynamic climbing rope and ascending a route while periodically attaching protection to the face of the route and...
fall, since the length of an arrested fall cannot exceed two times the length of the rope. Normally, a factor-2 fall can occur only when a lead climber who has placed no protection
Protection (climbing)
To make climbing as safe as possible, most climbers use protection, a term used to describe the equipment used to prevent injury to themselves and others.-Types of climbing:...
falls past the belayer (two times the distance of the rope length between them), or the anchor if the climber is solo climbing the route using a self-belay. As soon as the climber clips the rope into protection above the belay, the distance of the potential fall as a function of rope length is lessened, and the fall factor drops below 2.
A fall of 20 feet is much more severe (exerts more force on the climber and climbing equipment) if it occurs with 10 feet of rope out (i.e. the climber has placed no protection and falls from 10 feet above the belayer to 10 feet below—a factor 2 fall) than if it occurs 100 feet above the belayer (a fall factor of 0.2), in which case the stretch of the rope more effectively cushions the fall.
Via ferrata
In falls occurring on a via ferrataVia ferrata
A via ferrata or klettersteig is a mountain route which is equipped with fixed cables, stemples, ladders, and bridges. The use of these allows otherwise isolated routes to be joined to create longer routes which are accessible to people with a wide range of climbing abilities...
, fall factors can be much higher. This is possible because the length of rope between harness and carabiner
Carabiner
A carabiner or karabiner is a metal loop with a sprung or screwed gate that is used to quickly and reversibly connect components in safety-critical systems. The word comes from "Karabinerhaken", meaning "hook for a carbine" in German.-Use:...
is short and fixed, while the distance the climber can fall depends on the gaps between anchor points of the safety cable.

