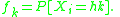
Panjer recursion
Encyclopedia
The Panjer recursion is an algorithm
to compute the probability distribution
of a compound random variable
where both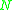
and 
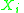are random variable
s and of special types. In more general cases the distribution of S is a compound distribution. The recursion for the special cases considered was introduced in a paper of Harry Panjer. It is heavily used in actuarial science
.
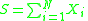where 
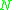and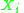 
fulfill the following preconditions.
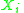to be i.i.d. and independent of 
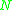. Furthermore the 
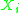have to be distributed on a lattice 
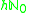with latticewidth 
.
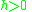, which is said to have a "claim number distribution", and which can take values 0, 1, 2, .... etc.. For the "Panjer recursion", the probability distribution
of N has to be a member of the Panjer class, otherwise known as the (a,b,0) class of distributions
. This class consists of all counting random variables which fulfill the following relation: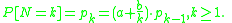
for some a and b which fulfill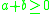
. The initial value 
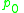is determined such that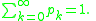 
The Panjer recursion makes use of this iterative relationship to specify a recursive way of constructing the probability distribution of S. In the following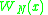
denotes the probability generating function of N: for this see the table in (a,b,0) class of distributions
.
.
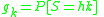The starting value is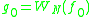
with the special cases
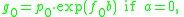
and
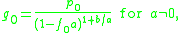
and proceed with
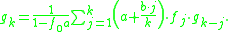
where 
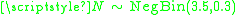and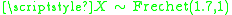 
with lattice width h = 0.04. (See Fréchet distribution.)
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to compute the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of a compound random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
-
.
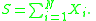where both
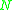and 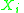are random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s and of special types. In more general cases the distribution of S is a compound distribution. The recursion for the special cases considered was introduced in a paper of Harry Panjer. It is heavily used in actuarial science
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
.
Preliminaries
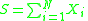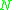We are interested in the compound random variable where and 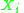fulfill the following preconditions.Claim size distribution
We assume the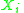 to be i.i.d. and independent of 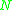. Furthermore the 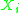have to be distributed on a lattice 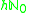with latticewidth .
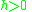Claim number distribution
The number of claims N is a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, which is said to have a "claim number distribution", and which can take values 0, 1, 2, .... etc.. For the "Panjer recursion", the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of N has to be a member of the Panjer class, otherwise known as the (a,b,0) class of distributions
(a,b,0) class of distributions
In probability theory, the distribution of a discrete random variable N is said to be a member of the class of distributions if its probability mass function obeyswhere p_k = P ....
. This class consists of all counting random variables which fulfill the following relation:
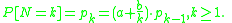
for some a and b which fulfill
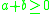. The initial value 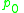is determined such that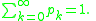 The Panjer recursion makes use of this iterative relationship to specify a recursive way of constructing the probability distribution of S. In the following
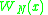denotes the probability generating function of N: for this see the table in (a,b,0) class of distributions(a,b,0) class of distributions
In probability theory, the distribution of a discrete random variable N is said to be a member of the class of distributions if its probability mass function obeyswhere p_k = P ....
.
Recursion
The algorithm now gives a recursion to compute the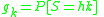.The starting value is
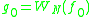with the special cases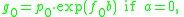and
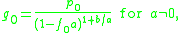
and proceed with
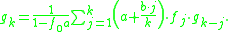
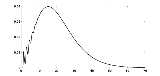
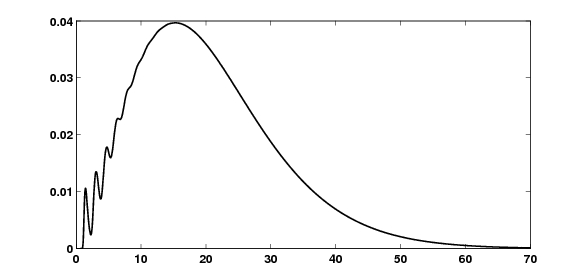
Example
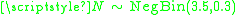The following example shows the approximated density of where and 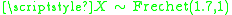with lattice width h = 0.04. (See Fréchet distribution.)