
Exponentially equivalent measures
Encyclopedia
In mathematics
, the notion of exponential equivalence of measures is a concept that describes how two sequences or families of probability measure
s are “the same” from the point of view of large deviations theory
.
and consider two one-parameter
families of probability measures on M, say (με)ε>0 and (νε)ε>0. These two families are said to be exponentially equivalent if there exist
such that
The two families of random variables (Yε)ε>0 and (Zε)ε>0 are also said to be exponentially equivalent.
I, and (με)ε>0 and (νε)ε>0 are exponentially equivalent, then the same large deviations principle holds for (νε)ε>0 with the same good rate function I.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the notion of exponential equivalence of measures is a concept that describes how two sequences or families of probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s are “the same” from the point of view of large deviations theory
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
.
Definition
Let (M, d) be a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
and consider two one-parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
families of probability measures on M, say (με)ε>0 and (νε)ε>0. These two families are said to be exponentially equivalent if there exist
- a one-parameter family of probability spaces ((Ω, Σε, Pε))ε>0,
- two families of M-valued random variables (Yε)ε>0 and (Zε)ε>0,
such that
- for each ε > 0, the Pε-law (i.e. the push-forward measure) of Yε is με, and the Pε-law of Zε is νε,
- for each δ > 0, “Yε and Zε are further than δ apart” is a Σε-measurable event, i.e.
-

- for each δ > 0,
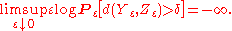
The two families of random variables (Yε)ε>0 and (Zε)ε>0 are also said to be exponentially equivalent.
Properties
The main use of exponential equivalence is that as far as large deviations principles are concerned, exponentially equivalent families of measures are indistinguishable. More precisely, if a large deviations principle holds for (με)ε>0 with good rate functionRate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
I, and (με)ε>0 and (νε)ε>0 are exponentially equivalent, then the same large deviations principle holds for (νε)ε>0 with the same good rate function I.

