
Exponential mechanism (differential privacy)
Encyclopedia
The exponential mechanism is a technique for designing differentially private algorithms developed by Frank McSherry and Kunal Talwar. Differential privacy
is a technique for releasing statistical information about a database without revealing information about its individual entries.
Most of the initial research in the field of differential privacy
revolved around real valued functions which have relatively low sensitivity
to change in the data of a single individual and whose usefulness is not hampered by small additive perturbations. A natural question is what happens in the situation when one wants to preserve more general sets of properties. The Exponential Mechanism helps to extend the notion of differential privacy to address these issues. Moreover, it describes a class of mechanisms that includes all possible differentially private mechanisms.
 inputs from domain
inputs from domain  , to a range
, to a range  . The map may be randomized, in which case each element of the domain
. The map may be randomized, in which case each element of the domain  corresponds to the probability distribution over the range
corresponds to the probability distribution over the range  . The privacy mechanism we are going to design makes no assumption about the nature of
. The privacy mechanism we are going to design makes no assumption about the nature of  and
and  apart from a base measure
apart from a base measure
 on
on  . Let us define a function
. Let us define a function  . Intuitively this function assigns score to the pair
. Intuitively this function assigns score to the pair 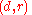 , where
, where  and
and 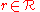 . The score reflects how appealing is the pair
. The score reflects how appealing is the pair  , i.e. the higher the score, the more appealing the pair is.
, i.e. the higher the score, the more appealing the pair is.
Once we are given the input , the mechanism's objective is to return an
, the mechanism's objective is to return an 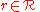 such that the function
such that the function 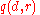 is approximately maximized. To achieve this, we set up the mechanism
is approximately maximized. To achieve this, we set up the mechanism 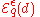 as follows:
as follows:
Definition: For any function , and a base measure
, and a base measure 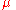 over
over  , we define:
, we define: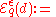 Choose
Choose  with probability proportional to
with probability proportional to 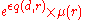 , where
, where  .
.
This definition implies the fact that the probability of returning an increases exponentially with the increase in the value of
increases exponentially with the increase in the value of 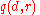 . For now if we ignore the base measure
. For now if we ignore the base measure  then the value
then the value  which maximizes
which maximizes 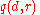 has the highest probability. Moreover we claim that this mechanism is differentially private. We will prove this claim shortly. One technicality that should be kept in mind is that in order to properly define
has the highest probability. Moreover we claim that this mechanism is differentially private. We will prove this claim shortly. One technicality that should be kept in mind is that in order to properly define  the
the 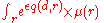 should be finite.
should be finite.
Theorem (Differential Privacy):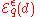 gives
gives  -differential privacy.
-differential privacy.
Proof: The probability density of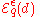 at
at  equals
equals .
.
Now, if a single change in changes
changes 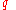 by at most
by at most  then the numerator can change at most by a factor of
then the numerator can change at most by a factor of  and the denominator minimum by a factor of
and the denominator minimum by a factor of 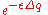 . Thus, the ratio of the new probability density (i.e. with new
. Thus, the ratio of the new probability density (i.e. with new 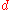 ) and the earlier one is at most
) and the earlier one is at most  .
.
 from the mechanism
from the mechanism 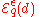 to nearly maximize
to nearly maximize  . If we consider
. If we consider  to be
to be  then we can show that the probability of the mechanism deviating from
then we can show that the probability of the mechanism deviating from  is low, as long as there is a sufficient mass (in terms of
is low, as long as there is a sufficient mass (in terms of  ) of values
) of values  with value
with value 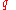 close to the optimum.
close to the optimum.
Lemma: Let and
and  , we have
, we have 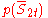 is at most
is at most  . The probability is taken over
. The probability is taken over  .
.
Proof: The probability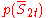 is at most
is at most 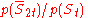 , as the denominator can be at most one. Since both the probabilities have the same normalizing term so,
, as the denominator can be at most one. Since both the probabilities have the same normalizing term so,

The value of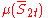 is at most one, and so this bound implies the lemma statement.
is at most one, and so this bound implies the lemma statement.
Theorem (Accuracy): For those values of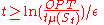 , we have
, we have  .
.
Proof: It follows from the previous lemma that the probability of the score being at least is
is  . By Hypothesis,
. By Hypothesis, 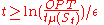 . Substituting the value of
. Substituting the value of  we get this probability to be at least
we get this probability to be at least  . Multiplying with
. Multiplying with  yields the desired bound.
yields the desired bound.
We can assume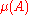 for
for  to be less than or equal to one in all the computations, because we can always normalize with
to be less than or equal to one in all the computations, because we can always normalize with 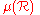 .
.
Definition (global sensitivity): The global sensitivity of a query is its maximum difference when evaluated on two neighbouring datasets
is its maximum difference when evaluated on two neighbouring datasets 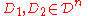 :
: .
.
Definition: A predicate query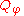 for any predicate
for any predicate 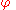 is defined to be
is defined to be .
.
Note that for any predicate
for any predicate 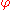 .
.
Definition (Usefulness): A mechanism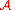 is
is  -useful for queries in class
-useful for queries in class  with probability
with probability  , if
, if  and every dataset
and every dataset  , for
, for 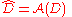 ,
,  .
.
Informally, it means that with high probability the query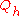 will behave in a similar way on the original dataset
will behave in a similar way on the original dataset  and on the synthetic dataset
and on the synthetic dataset  .
.
Let us consider a common problem in Data Mining. Assume there is a database with
with  entries. Each entry consist of
entries. Each entry consist of  -tuples of the form
-tuples of the form  where
where 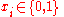 . Now, a user wants to learn a linear halfspace
. Now, a user wants to learn a linear halfspace
of the form . In essence the user wants to figure out the values of
. In essence the user wants to figure out the values of  such that maximum number of tuples in the database satisfy the inequality. The algorithm we describe below can generate a synthetic database
such that maximum number of tuples in the database satisfy the inequality. The algorithm we describe below can generate a synthetic database  which will allow the user to learn (approximately) the same linear half-space while querying on this synthetic database. The motivation for such an algorithm being that the new database will be generated in a differentially private manner and thus asssure privacy to the individual records in the database
which will allow the user to learn (approximately) the same linear half-space while querying on this synthetic database. The motivation for such an algorithm being that the new database will be generated in a differentially private manner and thus asssure privacy to the individual records in the database  .
.
In this section we show that it is possible to release a dataset which is useful for concepts from a polynomial VC-Dimension class and at the same time adhere to -differential privacy as long as the size of the original dataset is at least polynomial on the VC-Dimension of the concept class. To state formally:
-differential privacy as long as the size of the original dataset is at least polynomial on the VC-Dimension of the concept class. To state formally:
Theorem: For any class of functions and any dataset
and any dataset 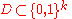 such that
such that
we can output an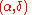 -useful dataset
-useful dataset  that preserves
that preserves  -differential privacy. As we had mentioned earlier the algorithm need not be efficient.
-differential privacy. As we had mentioned earlier the algorithm need not be efficient.
One interesting fact is that the algorithm which we are going to develop generates a synthetic dataset whose size is independent of the original dataset; in fact, it only depends on the VC-dimension
of the concept class and the parameter . The algorithm outputs a dataset of size
. The algorithm outputs a dataset of size 
We borrow the Uniform Convergence Theorem from combinatorics
and state a corollary of it which aligns to our need.
Lemma: Given any dataset there exists a dataset
there exists a dataset  of size
of size 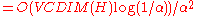 such that
such that  .
.
Proof:
We know from the uniform convergence theorem that,
 for some
for some  ,
,
where probability is over the distribution of the dataset.
Thus, if the RHS is less than one then we know for sure that the data set exists. To bound the RHS to less than one we need
exists. To bound the RHS to less than one we need  , where
, where  is some positive constant. Since we stated earlier that we will output a dataset of size
is some positive constant. Since we stated earlier that we will output a dataset of size 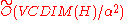 , so using this bound on
, so using this bound on  we get
we get 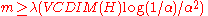 . Hence the lemma.
. Hence the lemma.
Now we invoke the Exponential Mechanism.
Definition: For any function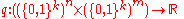 and input dataset
and input dataset  , the Exponential mechanism outputs each dataset
, the Exponential mechanism outputs each dataset  with probability proportional to
with probability proportional to  .
.
From the Exponential Mechanism we know this preserves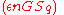 -differential privacy.
-differential privacy.
Lets get back to the proof of the Theorem.
We define .
.
To show that the mechanism satisfies the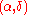 -usefulness, we should show that it outputs some dataset
-usefulness, we should show that it outputs some dataset  with
with 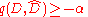 with probability
with probability  .
.
There are at most output datasets and the probability that
output datasets and the probability that 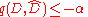 is at most proportional to
is at most proportional to 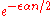 . Thus by union bound, the probability of outputting any such dataset
. Thus by union bound, the probability of outputting any such dataset  is at most proportional to
is at most proportional to  .
.
Again, we know that there exists some dataset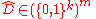 for which
for which  . Therefore, such a dataset is output with probability at least proportional to
. Therefore, such a dataset is output with probability at least proportional to  .
.
Let, the event that the Exponential mechanism outputs some dataset
the event that the Exponential mechanism outputs some dataset  such that
such that  .
.
 the event that the Exponential mechanism outputs some dataset
the event that the Exponential mechanism outputs some dataset  such that
such that 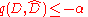 .
.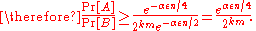
Now setting this quantity to be at least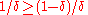 , we find that it suffices to have
, we find that it suffices to have .
.
And hence we prove the theorem.
and classification algorithms. In the case of auctions the Exponential Mechanism helps to achieve a truthful auction setting.
Differential privacy
Differential privacy aims to provide means to maximize the accuracy of queries from statistical databases while minimizing the chances of identifying its records.- Situation :...
is a technique for releasing statistical information about a database without revealing information about its individual entries.
Most of the initial research in the field of differential privacy
Differential privacy
Differential privacy aims to provide means to maximize the accuracy of queries from statistical databases while minimizing the chances of identifying its records.- Situation :...
revolved around real valued functions which have relatively low sensitivity
Differential privacy
Differential privacy aims to provide means to maximize the accuracy of queries from statistical databases while minimizing the chances of identifying its records.- Situation :...
to change in the data of a single individual and whose usefulness is not hampered by small additive perturbations. A natural question is what happens in the situation when one wants to preserve more general sets of properties. The Exponential Mechanism helps to extend the notion of differential privacy to address these issues. Moreover, it describes a class of mechanisms that includes all possible differentially private mechanisms.
Algorithm
In very generic terms a privacy mechanism maps a set of inputs from domain
inputs from domain  , to a range
, to a range  . The map may be randomized, in which case each element of the domain
. The map may be randomized, in which case each element of the domain  corresponds to the probability distribution over the range
corresponds to the probability distribution over the range  . The privacy mechanism we are going to design makes no assumption about the nature of
. The privacy mechanism we are going to design makes no assumption about the nature of  and
and  apart from a base measure
apart from a base measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
 on
on  . Let us define a function
. Let us define a function  . Intuitively this function assigns score to the pair
. Intuitively this function assigns score to the pair 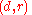 , where
, where  and
and 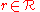 . The score reflects how appealing is the pair
. The score reflects how appealing is the pair  , i.e. the higher the score, the more appealing the pair is.
, i.e. the higher the score, the more appealing the pair is.Once we are given the input
 , the mechanism's objective is to return an
, the mechanism's objective is to return an 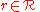 such that the function
such that the function 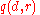 is approximately maximized. To achieve this, we set up the mechanism
is approximately maximized. To achieve this, we set up the mechanism 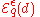 as follows:
as follows: Definition: For any function
 , and a base measure
, and a base measure 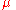 over
over  , we define:
, we define: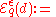 Choose
Choose  with probability proportional to
with probability proportional to 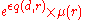 , where
, where  .
.This definition implies the fact that the probability of returning an
 increases exponentially with the increase in the value of
increases exponentially with the increase in the value of 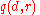 . For now if we ignore the base measure
. For now if we ignore the base measure  then the value
then the value  which maximizes
which maximizes 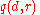 has the highest probability. Moreover we claim that this mechanism is differentially private. We will prove this claim shortly. One technicality that should be kept in mind is that in order to properly define
has the highest probability. Moreover we claim that this mechanism is differentially private. We will prove this claim shortly. One technicality that should be kept in mind is that in order to properly define  the
the 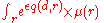 should be finite.
should be finite.Theorem (Differential Privacy):
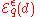 gives
gives  -differential privacy.
-differential privacy.Proof: The probability density of
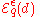 at
at  equals
equals .
.Now, if a single change in
 changes
changes 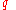 by at most
by at most  then the numerator can change at most by a factor of
then the numerator can change at most by a factor of  and the denominator minimum by a factor of
and the denominator minimum by a factor of 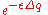 . Thus, the ratio of the new probability density (i.e. with new
. Thus, the ratio of the new probability density (i.e. with new 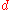 ) and the earlier one is at most
) and the earlier one is at most  .
.Accuracy
We would ideally want the random draws of from the mechanism
from the mechanism 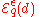 to nearly maximize
to nearly maximize  . If we consider
. If we consider  to be
to be  then we can show that the probability of the mechanism deviating from
then we can show that the probability of the mechanism deviating from  is low, as long as there is a sufficient mass (in terms of
is low, as long as there is a sufficient mass (in terms of  ) of values
) of values  with value
with value 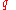 close to the optimum.
close to the optimum.Lemma: Let
 and
and  , we have
, we have 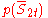 is at most
is at most  . The probability is taken over
. The probability is taken over  .
.Proof: The probability
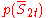 is at most
is at most 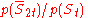 , as the denominator can be at most one. Since both the probabilities have the same normalizing term so,
, as the denominator can be at most one. Since both the probabilities have the same normalizing term so,
The value of
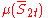 is at most one, and so this bound implies the lemma statement.
is at most one, and so this bound implies the lemma statement.Theorem (Accuracy): For those values of
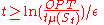 , we have
, we have  .
.Proof: It follows from the previous lemma that the probability of the score being at least
 is
is  . By Hypothesis,
. By Hypothesis, 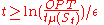 . Substituting the value of
. Substituting the value of  we get this probability to be at least
we get this probability to be at least  . Multiplying with
. Multiplying with  yields the desired bound.
yields the desired bound.We can assume
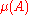 for
for  to be less than or equal to one in all the computations, because we can always normalize with
to be less than or equal to one in all the computations, because we can always normalize with 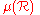 .
.Example application of the exponential mechanism
Before we get into the details of the example let us define some terms which we will be using extensively throughout our discussion.Definition (global sensitivity): The global sensitivity of a query
 is its maximum difference when evaluated on two neighbouring datasets
is its maximum difference when evaluated on two neighbouring datasets 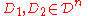 :
: .
.Definition: A predicate query
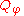 for any predicate
for any predicate 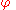 is defined to be
is defined to be .
.Note that
 for any predicate
for any predicate 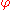 .
.Release mechanism
The following is due to Avrim Blum, Katrina Ligett and Aaron Roth.Definition (Usefulness): A mechanism
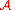 is
is  -useful for queries in class
-useful for queries in class  with probability
with probability  , if
, if  and every dataset
and every dataset  , for
, for 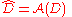 ,
,  .
.Informally, it means that with high probability the query
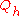 will behave in a similar way on the original dataset
will behave in a similar way on the original dataset  and on the synthetic dataset
and on the synthetic dataset  .
. Let us consider a common problem in Data Mining. Assume there is a database
 with
with  entries. Each entry consist of
entries. Each entry consist of  -tuples of the form
-tuples of the form  where
where 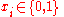 . Now, a user wants to learn a linear halfspace
. Now, a user wants to learn a linear halfspaceHalf-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
of the form
 . In essence the user wants to figure out the values of
. In essence the user wants to figure out the values of  such that maximum number of tuples in the database satisfy the inequality. The algorithm we describe below can generate a synthetic database
such that maximum number of tuples in the database satisfy the inequality. The algorithm we describe below can generate a synthetic database  which will allow the user to learn (approximately) the same linear half-space while querying on this synthetic database. The motivation for such an algorithm being that the new database will be generated in a differentially private manner and thus asssure privacy to the individual records in the database
which will allow the user to learn (approximately) the same linear half-space while querying on this synthetic database. The motivation for such an algorithm being that the new database will be generated in a differentially private manner and thus asssure privacy to the individual records in the database  .
.In this section we show that it is possible to release a dataset which is useful for concepts from a polynomial VC-Dimension class and at the same time adhere to
 -differential privacy as long as the size of the original dataset is at least polynomial on the VC-Dimension of the concept class. To state formally:
-differential privacy as long as the size of the original dataset is at least polynomial on the VC-Dimension of the concept class. To state formally:Theorem: For any class of functions
 and any dataset
and any dataset 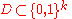 such that
such that
we can output an
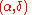 -useful dataset
-useful dataset  that preserves
that preserves  -differential privacy. As we had mentioned earlier the algorithm need not be efficient.
-differential privacy. As we had mentioned earlier the algorithm need not be efficient.One interesting fact is that the algorithm which we are going to develop generates a synthetic dataset whose size is independent of the original dataset; in fact, it only depends on the VC-dimension
VC dimension
In statistical learning theory, or sometimes computational learning theory, the VC dimension is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter...
of the concept class and the parameter
 . The algorithm outputs a dataset of size
. The algorithm outputs a dataset of size 
We borrow the Uniform Convergence Theorem from combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
and state a corollary of it which aligns to our need.
Lemma: Given any dataset
 there exists a dataset
there exists a dataset  of size
of size 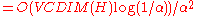 such that
such that  .
.Proof:
We know from the uniform convergence theorem that,
 for some
for some  ,
,where probability is over the distribution of the dataset.
Thus, if the RHS is less than one then we know for sure that the data set
 exists. To bound the RHS to less than one we need
exists. To bound the RHS to less than one we need  , where
, where  is some positive constant. Since we stated earlier that we will output a dataset of size
is some positive constant. Since we stated earlier that we will output a dataset of size 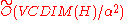 , so using this bound on
, so using this bound on  we get
we get 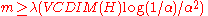 . Hence the lemma.
. Hence the lemma.Now we invoke the Exponential Mechanism.
Definition: For any function
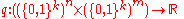 and input dataset
and input dataset  , the Exponential mechanism outputs each dataset
, the Exponential mechanism outputs each dataset  with probability proportional to
with probability proportional to  .
.From the Exponential Mechanism we know this preserves
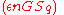 -differential privacy.
-differential privacy.Lets get back to the proof of the Theorem.
We define
 .
. To show that the mechanism satisfies the
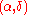 -usefulness, we should show that it outputs some dataset
-usefulness, we should show that it outputs some dataset  with
with 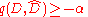 with probability
with probability  .
.There are at most
 output datasets and the probability that
output datasets and the probability that 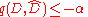 is at most proportional to
is at most proportional to 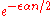 . Thus by union bound, the probability of outputting any such dataset
. Thus by union bound, the probability of outputting any such dataset  is at most proportional to
is at most proportional to  .
.Again, we know that there exists some dataset
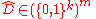 for which
for which  . Therefore, such a dataset is output with probability at least proportional to
. Therefore, such a dataset is output with probability at least proportional to  .
. Let,
 the event that the Exponential mechanism outputs some dataset
the event that the Exponential mechanism outputs some dataset  such that
such that  .
.  the event that the Exponential mechanism outputs some dataset
the event that the Exponential mechanism outputs some dataset  such that
such that 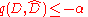 .
.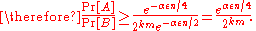
Now setting this quantity to be at least
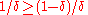 , we find that it suffices to have
, we find that it suffices to have .
.And hence we prove the theorem.
The Exponential Mechanism in other domains
We just showed an example of the usage of Exponential Mechanism where one can output a synthetic dataset in a differentially private manner and can use the dataset to answer queries with good accuracy. Apart from these kinds of setting, the Exponential Mechanism has also been studied in the context of auction theoryAuction theory
Auction theory is an applied branch of economics which deals with how people act in auction markets and researches the properties of auction markets. There are many possible designs for an auction and typical issues studied by auction theorists include the efficiency of a given auction design,...
and classification algorithms. In the case of auctions the Exponential Mechanism helps to achieve a truthful auction setting.

