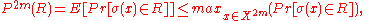Uniform convergence (combinatorics)
Encyclopedia
For a class of predicates  defined on a set
defined on a set 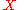 and a set of samples
and a set of samples  , where
, where 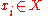 , the empirical frequency of
, the empirical frequency of 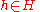 on
on  is
is 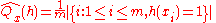 . The Uniform Convergence Theorem states, roughly,that if
. The Uniform Convergence Theorem states, roughly,that if  is "simple" and we draw samples independently (with replacement) from
is "simple" and we draw samples independently (with replacement) from 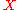 according to a distribution
according to a distribution 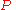 , then with high probability all the empirical frequency will be close to its expectation, where the expectation is given by
, then with high probability all the empirical frequency will be close to its expectation, where the expectation is given by 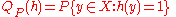 . Here "simple" means that the Vapnik-Chernovenkis dimension of the class
. Here "simple" means that the Vapnik-Chernovenkis dimension of the class  is small relative to the size of the sample.
is small relative to the size of the sample.
In other words, a sufficiently simple collection of functions behaves roughly the same on a small random sample as it does on the distribution as a whole.
 is a set of
is a set of 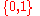 -valued functions defined on a set
-valued functions defined on a set 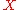 and
and 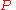 is a probability distribution on
is a probability distribution on 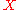 then for
then for  and
and  a positive integer, we have,
a positive integer, we have,
where, for any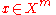 ,
,
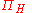 is defined as: For any
is defined as: For any 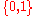 -valued functions
-valued functions  over
over 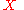 and
and  ,
,
And for any natural number the shattering number
the shattering number 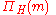 is defined as.
is defined as.
From the point of Learning Theory one can consider to be the Concept/Hypothesis
to be the Concept/Hypothesis
class defined over the instance set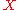 . Before getting into the details of the proof of the theorem we will state Sauer's Lemma which we will need in our proof.
. Before getting into the details of the proof of the theorem we will state Sauer's Lemma which we will need in our proof.
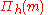 to the VC Dimension.
to the VC Dimension.
Lemma: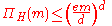 , where
, where 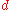 is the VC Dimension
is the VC Dimension
of the concept class .
.
Corollary: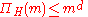 .
.
We present the technical details of the proof.
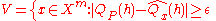 for some
for some  and
and
Then for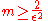 ,
, 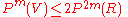 .
.
Proof:
By the triangle inequality,
if and
and 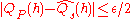 then
then 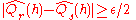 .
.
Therefore,
Now for fix an
fix an  such that
such that  . For this
. For this  , we shall show that
, we shall show that
Thus for any ,
, 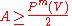 and hence
and hence 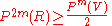 . And hence we perform the first step of our high level idea.
. And hence we perform the first step of our high level idea.
Notice,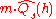 is a binomial random variable with expectation
is a binomial random variable with expectation 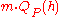 and variance
and variance 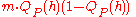 . By Chebyshev's inequality
. By Chebyshev's inequality
we get,
 be the set of all permutations of
be the set of all permutations of  that swaps
that swaps 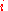 and
and 
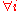 in some subset of
in some subset of  .
.
Lemma: Let be any subset of
be any subset of  and
and 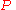 any probability distribution on
any probability distribution on 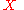 . Then,
. Then,
where the expectation is over chosen according to
chosen according to 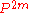 , and the probability is over
, and the probability is over  chosen uniformly from
chosen uniformly from  .
.
Proof:
For any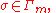
The maximum is guaranteed to exist since there is only a finite set of values that probability under a random permutation can take.
Proof:
Let us define and
and  which is atmost
which is atmost  . This means there are functions
. This means there are functions  such that for any
such that for any  between
between  and
and  with
with 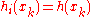 for
for  .
.
We see that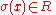 iff for some
iff for some  in
in  satisfies,
satisfies,
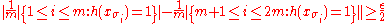 .
.
Hence if we define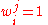 if
if 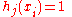 and
and 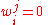 otherwise.
otherwise.
For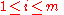 and
and 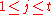 , we have that
, we have that 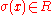 iff for some
iff for some  in
in  satisfies
satisfies 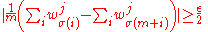 . By union bound we get,
. By union bound we get,
Since, the distribution over the permutations is uniform for each
is uniform for each 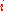 , so
, so 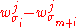 equals
equals 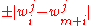 , with equal probability.
, with equal probability.
Thus,
where the probability on the right is over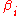 and both the possibilities are equally likely. By Hoeffding's inequality
and both the possibilities are equally likely. By Hoeffding's inequality
, this is at most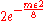 .
.
Finally, combining all the three parts of the proof we get the Uniform Convergence Theorem.
 defined on a set
defined on a set 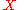 and a set of samples
and a set of samples  , where
, where 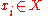 , the empirical frequency of
, the empirical frequency of 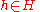 on
on  is
is 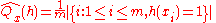 . The Uniform Convergence Theorem states, roughly,that if
. The Uniform Convergence Theorem states, roughly,that if  is "simple" and we draw samples independently (with replacement) from
is "simple" and we draw samples independently (with replacement) from 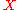 according to a distribution
according to a distribution 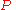 , then with high probability all the empirical frequency will be close to its expectation, where the expectation is given by
, then with high probability all the empirical frequency will be close to its expectation, where the expectation is given by 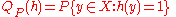 . Here "simple" means that the Vapnik-Chernovenkis dimension of the class
. Here "simple" means that the Vapnik-Chernovenkis dimension of the class  is small relative to the size of the sample.
is small relative to the size of the sample.In other words, a sufficiently simple collection of functions behaves roughly the same on a small random sample as it does on the distribution as a whole.
Uniform convergence theorem statement
If is a set of
is a set of 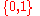 -valued functions defined on a set
-valued functions defined on a set 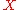 and
and 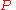 is a probability distribution on
is a probability distribution on 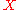 then for
then for  and
and  a positive integer, we have,
a positive integer, we have,-
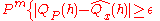 for some
for some 
where, for any
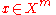 ,
,
-
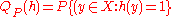 ,
, -
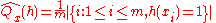 and
and 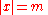 .
.  indicates that the probability is taken over
indicates that the probability is taken over  consisting of
consisting of  i.i.d. draws from the distribution
i.i.d. draws from the distribution 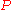 .
.
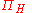 is defined as: For any
is defined as: For any 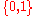 -valued functions
-valued functions  over
over 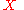 and
and  ,
,
-
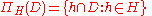 .
.
And for any natural number
 the shattering number
the shattering number 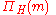 is defined as.
is defined as.
-
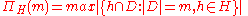 .
.
From the point of Learning Theory one can consider
 to be the Concept/Hypothesis
to be the Concept/HypothesisConcept class
A concept over a domain X is a total Boolean function over X. A concept class is a class of concepts. Concept class is a subject of computational learning theory....
class defined over the instance set
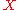 . Before getting into the details of the proof of the theorem we will state Sauer's Lemma which we will need in our proof.
. Before getting into the details of the proof of the theorem we will state Sauer's Lemma which we will need in our proof.Sauer's lemma:
Sauer's Lemma relates the shattering number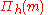 to the VC Dimension.
to the VC Dimension. Lemma:
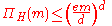 , where
, where 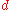 is the VC Dimension
is the VC DimensionVC dimension
In statistical learning theory, or sometimes computational learning theory, the VC dimension is a measure of the capacity of a statistical classification algorithm, defined as the cardinality of the largest set of points that the algorithm can shatter...
of the concept class
 .
.Corollary:
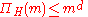 .
.Proof of uniform convergence theorem
Before we get into the details of the proof of the Uniform Convergence Theorem we will present a high level overview of the proof.- Symmetrization: We transform the problem of analyzing
 into the problem of analyzing
into the problem of analyzing 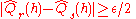 , where
, where  and
and  are i.i.d samples of size
are i.i.d samples of size  drawn according to the distribution
drawn according to the distribution 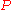 . One can view
. One can view  as the original randomly drawn sample of length
as the original randomly drawn sample of length  , while
, while  may be thought as the testing sample which is used to estimate
may be thought as the testing sample which is used to estimate 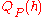 .
. - Permutation: Since
 and
and  are picked identically and independently, so swapping elements between them will not change the probability distribution on
are picked identically and independently, so swapping elements between them will not change the probability distribution on  and
and  . So, we will try to bound the probability of
. So, we will try to bound the probability of 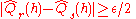 for some
for some 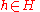 by considering the effect of a specific collection of permutations of the joint sample
by considering the effect of a specific collection of permutations of the joint sample 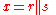 . Specifically, we consider permutations
. Specifically, we consider permutations 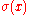 which swap
which swap 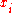 and
and  in some subset of
in some subset of  . The symbol
. The symbol  means the concatenation of
means the concatenation of  and
and  .
. - Reduction to a finite class: We can now restrict the function class
 to a fixed joint sample and hence, if
to a fixed joint sample and hence, if  has finite VC Dimension, it reduces to the problem to one involving a finite function class.
has finite VC Dimension, it reduces to the problem to one involving a finite function class.
We present the technical details of the proof.
Symmetrization
Lemma: Let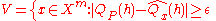 for some
for some  and
and
-
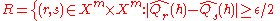 for some
for some 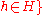 .
.
Then for
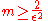 ,
, 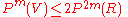 .
.Proof:
By the triangle inequality,
if
 and
and 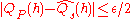 then
then 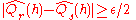 .
.Therefore,
-
 and
and 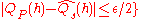
-
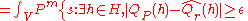 and
and 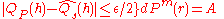 [since
[since  and
and  are independent].
are independent].
Now for
 fix an
fix an  such that
such that  . For this
. For this  , we shall show that
, we shall show that
-
 .
.
Thus for any
 ,
, 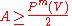 and hence
and hence 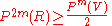 . And hence we perform the first step of our high level idea.
. And hence we perform the first step of our high level idea. Notice,
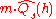 is a binomial random variable with expectation
is a binomial random variable with expectation 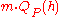 and variance
and variance 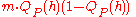 . By Chebyshev's inequality
. By Chebyshev's inequalityChebyshev's inequality
In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
we get,
-
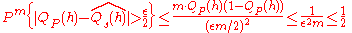 for the mentioned bound on
for the mentioned bound on  . Here we use the fact that
. Here we use the fact that 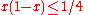 for
for  .
.
Permutations
Let be the set of all permutations of
be the set of all permutations of  that swaps
that swaps 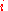 and
and 
 in some subset of
in some subset of  .
.Lemma: Let
 be any subset of
be any subset of  and
and 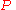 any probability distribution on
any probability distribution on 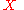 . Then,
. Then,
where the expectation is over
 chosen according to
chosen according to 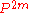 , and the probability is over
, and the probability is over  chosen uniformly from
chosen uniformly from  .
.Proof:
For any
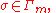
-
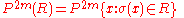 [since coordinate permutations preserve the product distribution
[since coordinate permutations preserve the product distribution 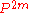 ].
]. -
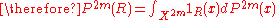
-
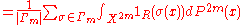
-
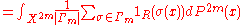 [Because
[Because 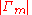 is finite]
is finite] -
 [The expectation]
[The expectation] -
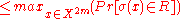 .
.
The maximum is guaranteed to exist since there is only a finite set of values that probability under a random permutation can take.
Reduction to a finite class
Lemma: Basing on the previous lemma,-
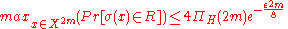 .
.
Proof:
Let us define
 and
and  which is atmost
which is atmost  . This means there are functions
. This means there are functions  such that for any
such that for any  between
between  and
and  with
with 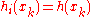 for
for  .
. We see that
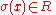 iff for some
iff for some  in
in  satisfies,
satisfies,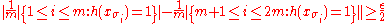 .
.Hence if we define
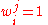 if
if 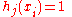 and
and 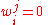 otherwise.
otherwise. For
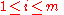 and
and 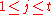 , we have that
, we have that 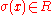 iff for some
iff for some  in
in  satisfies
satisfies 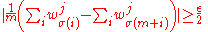 . By union bound we get,
. By union bound we get,
-
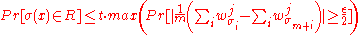
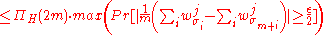 .
.
Since, the distribution over the permutations
 is uniform for each
is uniform for each 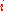 , so
, so 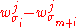 equals
equals 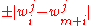 , with equal probability.
, with equal probability.Thus,
-
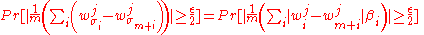 ,
,
where the probability on the right is over
 and both the possibilities are equally likely. By Hoeffding's inequality
and both the possibilities are equally likely. By Hoeffding's inequalityHoeffding's inequality
In probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
, this is at most
 .
.Finally, combining all the three parts of the proof we get the Uniform Convergence Theorem.