Explained sum of squares
Encyclopedia
In statistics
, the explained sum of squares (ESS) is a quantity used in describing how well a model, often a regression model
, represents the data being modelled. In particular, the explained sum of squares measures how much variation there is in the modelled values and this is compared to the total sum of squares
, which measures how much variation there is in the observed data, and to the residual sum of squares
, which measures the variation in the modelling errors.
s, i indexes the observations from 1 to n, and εi is the i th value of the error term. In general, the greater the ESS, the better the estimated model performs.
If
and 
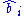are the estimated coefficient
s, then
is the i th predicted value of the response variable. The ESS is the sum of the squares of the differences of the predicted values and the mean value of the response variable:
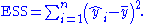
In general: total sum of squares
= explained sum of squares + residual sum of squares
.
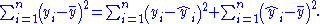
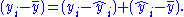
Square both sides and sum over all i:
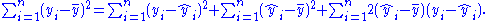
Simple linear regression
gives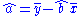
. What follows depends on this.
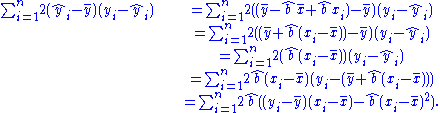
Again simple linear regression
gives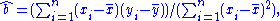
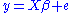
where y is an n × 1 vector of dependent variable observations, each column of the n × k matrix X is a vector of observations on one of the k explanators,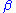
is a k × 1 vector of true coefficients, and e is an n× 1 vector of the true underlying errors. The ordinary least squares
estimator for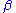
is
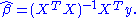
The residual vector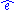
is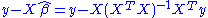 
, so the residual sum of squares 
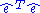is, after simplification,
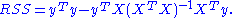
Denote as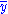
the constant vector all of whose elements are the sample mean 
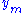of the dependent variable values in the vector y. Then the total sum of squares is
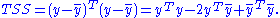
The explained sum of squares, defined as the sum of squared deviations of the predicted values from the observed mean of y, is
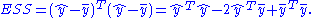
Using
in this, and simplifying to obtain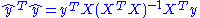 
, gives the result that TSS = ESS + RSS if and only if 
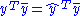. The left side of this is 
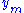times the sum of the elements of y, and the right side is 
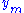times the sum of the elements of 
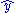, so the condition is that the sum of the elements of y equals the sum of the elements of 
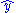, or equivalently that the sum of the prediction errors (residuals) 
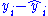is zero. This can be seen to be true by noting the well-known OLS property that the k × 1 vector 
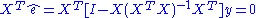: since the first column of X is a vector of ones, the first element of this vector 
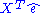is the sum of the residuals and is equal to zero. This proves that the condition holds for the result that TSS = ESS + RSS.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the explained sum of squares (ESS) is a quantity used in describing how well a model, often a regression model
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, represents the data being modelled. In particular, the explained sum of squares measures how much variation there is in the modelled values and this is compared to the total sum of squares
Total sum of squares
In statistical data analysis the total sum of squares is a quantity that appears as part of a standard way of presenting results of such analyses...
, which measures how much variation there is in the observed data, and to the residual sum of squares
Residual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
, which measures the variation in the modelling errors.
Definition
The explained sum of squares (ESS) is the sum of the squares of the deviations of the predicted values from the mean value of a response variable, in a standard regression model — for example, , where yi is the i th observation of the response variable, xji is the i th observation of the j th explanatory variable, a and bi are coefficientCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s, i indexes the observations from 1 to n, and εi is the i th value of the error term. In general, the greater the ESS, the better the estimated model performs.
If
and 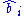are the estimated coefficientCoefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s, then
is the i th predicted value of the response variable. The ESS is the sum of the squares of the differences of the predicted values and the mean value of the response variable:
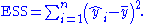
In general: total sum of squares
Total sum of squares
In statistical data analysis the total sum of squares is a quantity that appears as part of a standard way of presenting results of such analyses...
= explained sum of squares + residual sum of squares
Residual sum of squares
In statistics, the residual sum of squares is the sum of squares of residuals. It is also known as the sum of squared residuals or the sum of squared errors of prediction . It is a measure of the discrepancy between the data and an estimation model...
.
Partitioning in simple linear regression
The following equality, stating that the total sum of squares equals the residual sum of squares plus the explained sum of squares, is generally true in simple linear regression: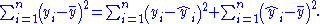Simple derivation
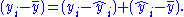
Square both sides and sum over all i:
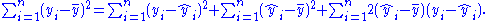
Simple linear regression
Simple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
gives
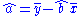. What follows depends on this.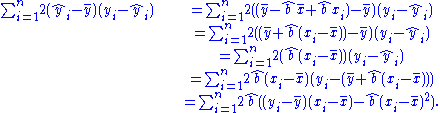Again simple linear regression
Simple linear regression
In statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
gives
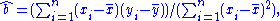
Partitioning in the general OLS model
The general regression model with n observations and k explanators, the first of which is a constant unit vector whose coefficient is the regression intercept, is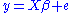where y is an n × 1 vector of dependent variable observations, each column of the n × k matrix X is a vector of observations on one of the k explanators,
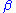is a k × 1 vector of true coefficients, and e is an n× 1 vector of the true underlying errors. The ordinary least squaresOrdinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
estimator for
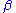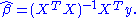
isThe residual vector
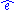is 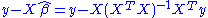, so the residual sum of squares 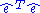is, after simplification,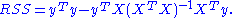Denote as
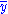the constant vector all of whose elements are the sample mean 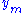of the dependent variable values in the vector y. Then the total sum of squares is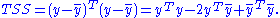The explained sum of squares, defined as the sum of squared deviations of the predicted values from the observed mean of y, is
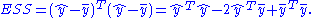
Using
in this, and simplifying to obtain 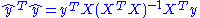, gives the result that TSS = ESS + RSS if and only if 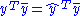. The left side of this is 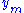times the sum of the elements of y, and the right side is 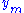times the sum of the elements of 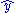, so the condition is that the sum of the elements of y equals the sum of the elements of 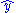, or equivalently that the sum of the prediction errors (residuals) 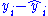is zero. This can be seen to be true by noting the well-known OLS property that the k × 1 vector 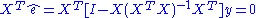: since the first column of X is a vector of ones, the first element of this vector 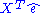is the sum of the residuals and is equal to zero. This proves that the condition holds for the result that TSS = ESS + RSS.