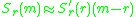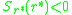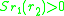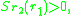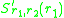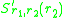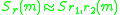Evolutionary invasion analysis
Encyclopedia
Evolutionary invasion analysis, also known as adaptive dynamics, is a set of techniques for studying long-term phenotypical evolution
developed during the 1990s. It incorporates the concept of frequency dependence
from game theory
but allows for more realistic ecological descriptions, as the traits vary continuously and gives rise to a non-linear invasion fitness (the classical fitness
concept is not directly applicable to situations with frequency dependence).
naturalist Charles Darwin in his 1859 book, On the Origin of Species. Though controversial at the time, the central ideas remain
virtually unchanged to this date, even though much more is now known
about the biological basis of inheritance. Darwin expressed his
arguments verbally, but many attempts have since then been made to
formalise the theory of evolution. The perhaps most well known are
population genetics
which aim to model the
biological basis of inheritance but usually at the expense of
ecological detail, quantitative genetics
which
incorporates quantitative traits influenced by genes at many loci and
evolutionary game theory which ignores genetic
detail but incorporates a high degree of ecological realism, in
particular that the success of any given strategy depends on the
frequency at which strategies are played in the population, a concept
known as frequency dependence.
Adaptive Dynamics is a set of techniques developed during the 1990s
for understanding the long-term consequences of small mutations in the
traits expressing the phenotype. They link population dynamics
to evolutionary dynamics
and incorporate and generalises the
fundamental idea of frequency dependent selection from game theory.
The number of papers using Adaptive Dynamics techniques is increasing
steadily as Adaptive Dynamics is gaining ground as a versatile tool
for evolutionary modelling.
population can be assumed to be in a dynamical equilibrium when new
mutants appear, and that the eventual fate of such mutants can be
inferred from their initial growth rate when rare in the environment
consisting of the resident. This rate is known as the invasion
exponent when measured as the initial exponential growth rate of
mutants, and as the basic reproductive number when it measures
the expected total number of offspring that a mutant individual will
produce in a lifetime. It can be thought of, and is indeed sometimes
also referred to, as the invasion fitness of mutants. In order to make use
of these ideas we require a mathematical model that explicitly
incorporates the traits undergoing evolutionary change. The model
should describe both the environment and the population dynamics given
the environment, but in many cases the variable part of the
environment consists only of the demography of the current
population. We then determine the invasion exponent, the initial
growth rate of a mutant invading the environment consisting of the
resident. Depending on the model, this can be trivial or very
difficult, but once determined, the Adaptive Dynamics techniques can be
applied independent of the model structure.
monomorphic. If not explicitly stated differently, we will assume that the
trait is a real number, and we will write r and m for the trait
value of the monomorphic resident population and that of an invading
mutant, respectively.
is defined as the expected growth
rate of an initially rare mutant in the environment set by the
resident (r), which simply means the frequency of each phenotype (trait
value) whenever this suffices to infer all other aspects of the
equilibrium environment, such as the demographic composition and the
availability of resources. For each r the invasion exponent can be
thought of as the fitness landscape experienced by an initially rare
mutant. The landscape changes with each successful invasion, as is the case in evolutionary game theory, but
in contrast with the classical view of evolution as an optimisation
process towards ever higher fitness.
We will always assume that the resident is at its demographic
attractor, and as a consequence
for all r,
as otherwise the population would grow indefinitely.
The selection gradient is defined as the slope of the invasion
exponent at
, 
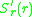. If the
sign of the invasion exponent is positive (negative) mutants with
slightly higher (lower) trait values may successfully invade. This
follows from the linear approximation
which holds whenever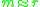
.
by a rare mutant. In a large (infinite) population only mutants with
trait values
for which 
is positive are able to
successfully invade. The generic outcome of an invasion is that the
mutant replaces the resident, and the fitness landscape as experienced
by a rare mutant changes. To determine the outcome of the resulting
series of invasions pairwise-invasibility plots (PIPs) are often used.
These show for each resident trait value
all mutant trait values
for which 
is positive. Note that
is zero at the diagonal 
. In PIPs the fitness landscapes as
experienced by a rare mutant correspond to
the vertical lines where the resident trait value
is constant.
determines the direction of
evolutionary change. If it is positive (negative) a mutant with a
slightly higher (lower) trait-value will generically invade and
replace the resident. But what will happen if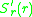
vanishes?
Seemingly evolution should come to a halt at such a point. While this
is a possible outcome, the general situation is more complex. Traits
or strategies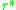
for which 
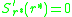, are known as
evolutionarily singular strategies. Near such points the fitness
landscape as experienced by a rare mutant is locally `flat'. There are three qualitatively
different ways in which this can occur. First, a degenerate case similar to the qubic where
finite evolutionary steps would lead past the local 'flatness'. Second, a fitness maximum which is known as an evolutionarily stable strategy
(ESS) and which, once established, cannot be invaded by nearby
mutants. Third, a fitness minimum
where disruptive selection will occur and the population branch into
two morphs. This process is known as evolutionary branching.
In a pairwise invasibility plot the singular strategies are found where the
boundary of the region of positive invasion fitness intersects the
diagonal.
Singular strategies can be located and classified once the
selection gradient is known. To locate singular strategies, it is
sufficient to find the points for which the selection gradient
vanishes, i.e. to find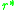
such that 
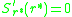. These can
be classified then using the second derivative test from basic
calculus. If the second derivative evaluated at
is negative
(positive) the strategy represents a local fitness maximum (minimum).
Hence, for an evolutionarily stable strategy
we have
If this does not hold the strategy is evolutionarily unstable and,
provided that it also convergence stable, evolutionary branching will
eventually occur. For a singular strategy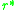
to be convergence
stable monomorphic populations with slightly lower or slightly higher
trait values must be invadable by mutants with trait values closer to
. That this can happen the selection gradient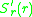 
in a
neighbourhood of
must be positive for 
and negative for
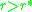. This means that the slope of 
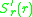as a function of 
at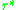
is negative, or equivalently
The criterion for convergence stability given above can also be
expressed using second derivatives of the invasion exponent, and the
classification can be refined to span more than the simple cases
considered here.
replaces the resident. However, other outcomes are also possible; in particular both the resident and the mutant
may persist, and the population then becomes dimorphic. Assuming that a
trait persists in the population if and only if its expected
growth-rate when rare is positive, the condition for coexistence among
two traits
and 
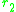is
and
where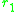
and 
are often referred to as morphs.
Such a pair is a protected dimorphism. The set of all protected
dimorphisms is known as the region of coexistence. Graphically,
the region consists of the overlapping parts when a pair-wise
invasibility plot is mirrored over the diagonal
straightforward manner, as the expected growth rate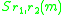
of a rare mutant in the environment set by the two morphs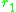
and
. The slope of the local fitness landscape for a mutant close to
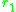or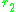 
is now given by the selection gradients
and
In practise, it is often difficult to determine the dimorphic
selection gradient and invasion exponent analytically, and one often
has to resort to numerical computations.
course of evolution is not unusual, but its significance depends on
whether selection is stabilising or disruptive. In the latter case,
the traits of the two morphs will diverge in a process often referred to
as evolutionary branching. Geritz 1998 presents a compelling
argument that disruptive selection only occurs near fitness minima. To
understand this heuristically consider a dimorphic population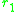
and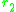
near a singular point. By continuity
and, since
the
fitness landscape for the dimorphic population must be a perturbation
of that for a monomorphic resident near the singular strategy.
plots. These show the region of coexistence, the direction of
evolutionary change and whether points where points where the
selection gradient vanishes are fitness maxima or minima. Evolution
may well lead the dimorphic population outside the region of
coexistence, in which case one morph is extinct and the population
once again becomes monomorphic.
and population dynamics
. As such, it can be very useful in investigating how evolution
affects the dynamics of populations
. One interesting finding to come out of this is that individual-level adaptation
can sometimes result in the extinction
of the whole population
/species
, a phenomenon known as evolutionary suicide
.
Evolution
Evolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
developed during the 1990s. It incorporates the concept of frequency dependence
Frequency dependent selection
Frequency-dependent selection is the term given to an evolutionary process where the fitness of a phenotype is dependent on its frequency relative to other phenotypes in a given population. In positive frequency-dependent selection the fitness of a phenotype increases as it becomes more common...
from game theory
Game theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
but allows for more realistic ecological descriptions, as the traits vary continuously and gives rise to a non-linear invasion fitness (the classical fitness
Fitness (biology)
Fitness is a central idea in evolutionary theory. It can be defined either with respect to a genotype or to a phenotype in a given environment...
concept is not directly applicable to situations with frequency dependence).
Introduction and background
The basic principle of evolution via natural selection, survival of the fittest, was outlined by thenaturalist Charles Darwin in his 1859 book, On the Origin of Species. Though controversial at the time, the central ideas remain
virtually unchanged to this date, even though much more is now known
about the biological basis of inheritance. Darwin expressed his
arguments verbally, but many attempts have since then been made to
formalise the theory of evolution. The perhaps most well known are
population genetics
Population genetics
Population genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
which aim to model the
biological basis of inheritance but usually at the expense of
ecological detail, quantitative genetics
Quantitative genetics
Quantitative genetics is the study of continuous traits and their underlying mechanisms. It is effectively an extension of simple Mendelian inheritance in that the combined effects of one or more genes and the environments in which they are expressed give rise to continuous distributions of...
which
incorporates quantitative traits influenced by genes at many loci and
evolutionary game theory which ignores genetic
detail but incorporates a high degree of ecological realism, in
particular that the success of any given strategy depends on the
frequency at which strategies are played in the population, a concept
known as frequency dependence.
Adaptive Dynamics is a set of techniques developed during the 1990s
for understanding the long-term consequences of small mutations in the
traits expressing the phenotype. They link population dynamics
Population dynamics
Population dynamics is the branch of life sciences that studies short-term and long-term changes in the size and age composition of populations, and the biological and environmental processes influencing those changes...
to evolutionary dynamics
Evolutionary dynamics
Evolutionary dynamics is the study of the mathematical principles according to which life has evolved and continues to evolve. In this area, Evolution has become a mathematical theory, and any idea of an evolutionary process or mechanism should be studied in the context of the mathematical...
and incorporate and generalises the
fundamental idea of frequency dependent selection from game theory.
The number of papers using Adaptive Dynamics techniques is increasing
steadily as Adaptive Dynamics is gaining ground as a versatile tool
for evolutionary modelling.
Fundamental ideas
Two fundamental ideas of Adaptive Dynamics are that the residentpopulation can be assumed to be in a dynamical equilibrium when new
mutants appear, and that the eventual fate of such mutants can be
inferred from their initial growth rate when rare in the environment
consisting of the resident. This rate is known as the invasion
exponent when measured as the initial exponential growth rate of
mutants, and as the basic reproductive number when it measures
the expected total number of offspring that a mutant individual will
produce in a lifetime. It can be thought of, and is indeed sometimes
also referred to, as the invasion fitness of mutants. In order to make use
of these ideas we require a mathematical model that explicitly
incorporates the traits undergoing evolutionary change. The model
should describe both the environment and the population dynamics given
the environment, but in many cases the variable part of the
environment consists only of the demography of the current
population. We then determine the invasion exponent, the initial
growth rate of a mutant invading the environment consisting of the
resident. Depending on the model, this can be trivial or very
difficult, but once determined, the Adaptive Dynamics techniques can be
applied independent of the model structure.
Monomorphic evolution
A population consisting of individuals with the same trait is calledmonomorphic. If not explicitly stated differently, we will assume that the
trait is a real number, and we will write r and m for the trait
value of the monomorphic resident population and that of an invading
mutant, respectively.
Invasion exponent and selection gradient
The invasion exponent is defined as the expected growthrate of an initially rare mutant in the environment set by the
resident (r), which simply means the frequency of each phenotype (trait
value) whenever this suffices to infer all other aspects of the
equilibrium environment, such as the demographic composition and the
availability of resources. For each r the invasion exponent can be
thought of as the fitness landscape experienced by an initially rare
mutant. The landscape changes with each successful invasion, as is the case in evolutionary game theory, but
in contrast with the classical view of evolution as an optimisation
process towards ever higher fitness.
We will always assume that the resident is at its demographic
attractor, and as a consequence
for all r,as otherwise the population would grow indefinitely.
The selection gradient is defined as the slope of the invasion
exponent at
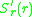, . If thesign of the invasion exponent is positive (negative) mutants with
slightly higher (lower) trait values may successfully invade. This
follows from the linear approximation
which holds whenever
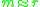.Pairwise-invasibility plots
The invasion exponent represents the fitness landscape as experiencedby a rare mutant. In a large (infinite) population only mutants with
trait values
for which is positive are able tosuccessfully invade. The generic outcome of an invasion is that the
mutant replaces the resident, and the fitness landscape as experienced
by a rare mutant changes. To determine the outcome of the resulting
series of invasions pairwise-invasibility plots (PIPs) are often used.
These show for each resident trait value
all mutant trait values for which is positive. Note that is zero at the diagonal . In PIPs the fitness landscapes asexperienced by a rare mutant correspond to
the vertical lines where the resident trait value
is constant.Evolutionarily singular strategies
The selection gradient determines the direction ofevolutionary change. If it is positive (negative) a mutant with a
slightly higher (lower) trait-value will generically invade and
replace the resident. But what will happen if
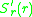vanishes?Seemingly evolution should come to a halt at such a point. While this
is a possible outcome, the general situation is more complex. Traits
or strategies
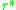for which 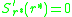, are known asevolutionarily singular strategies. Near such points the fitness
landscape as experienced by a rare mutant is locally `flat'. There are three qualitatively
different ways in which this can occur. First, a degenerate case similar to the qubic where
finite evolutionary steps would lead past the local 'flatness'. Second, a fitness maximum which is known as an evolutionarily stable strategy
Evolutionarily stable strategy
In game theory and behavioural ecology, an evolutionarily stable strategy , which is sometimes also called an evolutionary stable strategy, is a strategy which, if adopted by a population of players, cannot be invaded by any alternative strategy that is initially rare. An ESS is an equilibrium...
(ESS) and which, once established, cannot be invaded by nearby
mutants. Third, a fitness minimum
where disruptive selection will occur and the population branch into
two morphs. This process is known as evolutionary branching.
In a pairwise invasibility plot the singular strategies are found where the
boundary of the region of positive invasion fitness intersects the
diagonal.
Singular strategies can be located and classified once the
selection gradient is known. To locate singular strategies, it is
sufficient to find the points for which the selection gradient
vanishes, i.e. to find
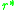such that 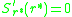. These canbe classified then using the second derivative test from basic
calculus. If the second derivative evaluated at
is negative(positive) the strategy represents a local fitness maximum (minimum).
Hence, for an evolutionarily stable strategy
we have
If this does not hold the strategy is evolutionarily unstable and,
provided that it also convergence stable, evolutionary branching will
eventually occur. For a singular strategy
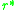to be convergencestable monomorphic populations with slightly lower or slightly higher
trait values must be invadable by mutants with trait values closer to
. That this can happen the selection gradient 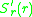in aneighbourhood of
must be positive for and negative for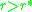. This means that the slope of 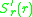as a function of at
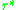is negative, or equivalently
The criterion for convergence stability given above can also be
expressed using second derivatives of the invasion exponent, and the
classification can be refined to span more than the simple cases
considered here.
Polymorphic evolution
The normal outcome of a successful invasion is that the mutantreplaces the resident. However, other outcomes are also possible; in particular both the resident and the mutant
may persist, and the population then becomes dimorphic. Assuming that a
trait persists in the population if and only if its expected
growth-rate when rare is positive, the condition for coexistence among
two traits
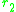and is
and
where
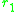and are often referred to as morphs.Such a pair is a protected dimorphism. The set of all protected
dimorphisms is known as the region of coexistence. Graphically,
the region consists of the overlapping parts when a pair-wise
invasibility plot is mirrored over the diagonal
Invasion exponent and selection gradients in polymorphic populations
The invasion exponent is generalised to dimorphic populations in astraightforward manner, as the expected growth rate
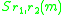
of a rare mutant in the environment set by the two morphs
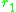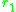and. The slope of the local fitness landscape for a mutant close to or 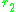is now given by the selection gradients
and
In practise, it is often difficult to determine the dimorphic
selection gradient and invasion exponent analytically, and one often
has to resort to numerical computations.
Evolutionary branching
The emergence of protected dimorphism near singular points during thecourse of evolution is not unusual, but its significance depends on
whether selection is stabilising or disruptive. In the latter case,
the traits of the two morphs will diverge in a process often referred to
as evolutionary branching. Geritz 1998 presents a compelling
argument that disruptive selection only occurs near fitness minima. To
understand this heuristically consider a dimorphic population
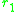
and
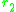near a singular point. By continuity
and, since
the
fitness landscape for the dimorphic population must be a perturbation
of that for a monomorphic resident near the singular strategy.
Trait evolution plots
Evolution after branching is illustrated using trait evolutionplots. These show the region of coexistence, the direction of
evolutionary change and whether points where points where the
selection gradient vanishes are fitness maxima or minima. Evolution
may well lead the dimorphic population outside the region of
coexistence, in which case one morph is extinct and the population
once again becomes monomorphic.
Other uses
Adaptive dynamics effectively combines game theoryGame theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
and population dynamics
Population dynamics
Population dynamics is the branch of life sciences that studies short-term and long-term changes in the size and age composition of populations, and the biological and environmental processes influencing those changes...
. As such, it can be very useful in investigating how evolution
Evolution
Evolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
affects the dynamics of populations
Population dynamics
Population dynamics is the branch of life sciences that studies short-term and long-term changes in the size and age composition of populations, and the biological and environmental processes influencing those changes...
. One interesting finding to come out of this is that individual-level adaptation
Adaptation
An adaptation in biology is a trait with a current functional role in the life history of an organism that is maintained and evolved by means of natural selection. An adaptation refers to both the current state of being adapted and to the dynamic evolutionary process that leads to the adaptation....
can sometimes result in the extinction
Extinction
In biology and ecology, extinction is the end of an organism or of a group of organisms , normally a species. The moment of extinction is generally considered to be the death of the last individual of the species, although the capacity to breed and recover may have been lost before this point...
of the whole population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
/species
Species
In biology, a species is one of the basic units of biological classification and a taxonomic rank. A species is often defined as a group of organisms capable of interbreeding and producing fertile offspring. While in many cases this definition is adequate, more precise or differing measures are...
, a phenomenon known as evolutionary suicide
Evolutionary suicide
Evolutionary suicide is an evolutionary mechanism where adaptation at the level of the individual results in a situation where the entire population goes extinct...
.
See also
- EvolutionEvolutionEvolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
- Game theoryGame theoryGame theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
- Population geneticsPopulation geneticsPopulation genetics is the study of allele frequency distribution and change under the influence of the four main evolutionary processes: natural selection, genetic drift, mutation and gene flow. It also takes into account the factors of recombination, population subdivision and population...
- Quantitative geneticsQuantitative geneticsQuantitative genetics is the study of continuous traits and their underlying mechanisms. It is effectively an extension of simple Mendelian inheritance in that the combined effects of one or more genes and the environments in which they are expressed give rise to continuous distributions of...
- Evolutionary dynamicsEvolutionary dynamicsEvolutionary dynamics is the study of the mathematical principles according to which life has evolved and continues to evolve. In this area, Evolution has become a mathematical theory, and any idea of an evolutionary process or mechanism should be studied in the context of the mathematical...
External links
- The Hitchhiker's guide to Adaptive Dynamics on which the first version of this article was based (GFDL).
- Adaptive Dynamics Papers, a comprehensive list of papers about Adaptive Dynamics.
- Christoph Hauert's applications to continuous games site: Java applets and tutorial.