Elliptic filter
Encyclopedia
An elliptic filter is a signal processing filter
with equalized ripple (equiripple) behavior in both the passband
and the stopband
. The amount of ripple in each band is independently adjustable, and no other filter of equal order can have a faster transition in gain
between the passband
and the stopband
, for the given values of ripple (whether the ripple is equalized or not). Alternatively, one may give up the ability to independently adjust the passband and stopband ripple, and instead design a filter which is maximally insensitive to component variations.
As the ripple in the stopband approaches zero, the filter becomes a type I Chebyshev filter
. As the ripple in the passband approaches zero, the filter becomes a type II Chebyshev filter
and finally, as both ripple values approach zero, the filter becomes a Butterworth filter
.
The gain of a lowpass elliptic filter as a function of angular frequency ω is given by:
where Rn is the nth-order elliptic rational function
(sometimes known as a Chebyshev rational function) and
is the cutoff frequency
is the ripple factor
is the selectivity factor
The value of the ripple factor specifies the passband ripple, while the combination of the ripple factor and the selectivity factor specify the stopband ripple.
.svg.png)
.svg.png)
.svg.png)
.svg.png)
The zeroes of the gain of an elliptic filter will coincide with the poles of the elliptic rational function, which are derived in the article on elliptic rational functions
.
The poles of the gain of an elliptic filter may be derived in a manner very similar to the derivation of the poles of the gain of a type I Chebyshev filter
. For simplicity, assume that the cutoff frequency is equal to unity. The poles
of the gain of the elliptical filter will be the zeroes of the denominator of the gain. Using the complex frequency 
this means that:
Defining
where cd is the Jacobi elliptic cosine function and using the definition of the elliptic rational functions yields:
where
and 
. Solving for w
where the multiple values of the inverse cd function are made explicit using the integer index m.
The poles of the elliptic gain function are then:
As is the case for the Chebyshev polynomials, this may be expressed in explicitly complex form
where
is a function of 
and 
and 
are the zeroes of the elliptic rational function. 
is expressible for all n in terms of Jacobi elliptic functions, or algebraically for some orders, especially orders 1,2, and 3. For orders 1 and 2 we have
where
The algebraic expression for
is rather involved (See ).
The nesting property of the elliptic rational functions
can be used to build up higher order expressions for
:
where
.
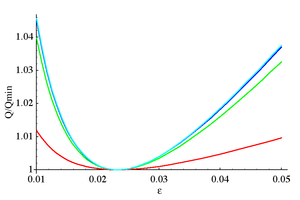See .
Elliptic filters are generally specified by requiring a particular value for the passband ripple, stopband ripple and the sharpness of the cutoff. This will generally specify a minimum value of the filter order which must be used. Another design consideration is the sensitivity of the gain function to the values of the electronic components used to build the filter. This sensitivity is inversely proportional to the quality factor (Q-factor) of the poles of the transfer function of the filter. The Q-factor of a pole is defined as:
and is a measure of the influence of the pole on the gain function. For an elliptic filter, it happens that, for a given order, there exists a relationship between the ripple factor and selectivity factor which simultaneously minimizes the Q-factor of all poles in the transfer function:
This results in a filter which is maximally insensitive to component variations, but the ability to independently specify the passband and stopband ripples will be lost. For such filters, as the order increases, the ripple in both bands will decrease and the rate of cutoff will increase. If one decides to use a minimum-Q elliptic filter in order to achieve a particular minimum ripple in the filter bands along with a particular rate of cutoff, the order needed will generally be greater than the order one would otherwise need without the minimum-Q restriction. An image of the absolute value of the gain will look very much like the image in the previous section, except that the poles are arranged in a circle rather than an ellipse. They will not be evenly spaced and there will be zeroes on the ω axis, unlike the Butterworth filter
, whose poles are also arranged in a circle.
As is clear from the image, elliptic filters are sharper than all the others, but they show ripples on the whole bandwidth.
Filter (signal processing)
In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
with equalized ripple (equiripple) behavior in both the passband
Passband
A passband is the range of frequencies or wavelengths that can pass through a filter without being attenuated.A bandpass filtered signal , is known as a bandpass signal, as opposed to a baseband signal....
and the stopband
Stopband
A stopband is a band of frequencies, between specified limits, through which a circuit, such as a filter or telephone circuit, does not allow signals to pass, or the attenuation is above the required stopband attenuation level...
. The amount of ripple in each band is independently adjustable, and no other filter of equal order can have a faster transition in gain
Gain
In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
between the passband
Passband
A passband is the range of frequencies or wavelengths that can pass through a filter without being attenuated.A bandpass filtered signal , is known as a bandpass signal, as opposed to a baseband signal....
and the stopband
Stopband
A stopband is a band of frequencies, between specified limits, through which a circuit, such as a filter or telephone circuit, does not allow signals to pass, or the attenuation is above the required stopband attenuation level...
, for the given values of ripple (whether the ripple is equalized or not). Alternatively, one may give up the ability to independently adjust the passband and stopband ripple, and instead design a filter which is maximally insensitive to component variations.
As the ripple in the stopband approaches zero, the filter becomes a type I Chebyshev filter
Chebyshev filter
Chebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
. As the ripple in the passband approaches zero, the filter becomes a type II Chebyshev filter
Chebyshev filter
Chebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
and finally, as both ripple values approach zero, the filter becomes a Butterworth filter
Butterworth filter
The Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
.
The gain of a lowpass elliptic filter as a function of angular frequency ω is given by:
where Rn is the nth-order elliptic rational function
Elliptic rational functions
In mathematics the elliptic rational functions are a sequence of rational functions with real coefficients. Elliptic rational functions are extensively used in the design of elliptic electronic filters...
(sometimes known as a Chebyshev rational function) and
is the cutoff frequency is the ripple factor is the selectivity factorThe value of the ripple factor specifies the passband ripple, while the combination of the ripple factor and the selectivity factor specify the stopband ripple.
Properties
- In the passband, the elliptic rational function varies between zero and unity. The passband of the gain therefore will vary between 1 and
.
- In the stopband, the elliptic rational function varies between infinity and the discrimination factor
which is defined as:
- The gain of the stopband therefore will vary between 0 and
.
- In the limit of
the elliptic rational function becomes a Chebyshev polynomial, and therefore the filter becomes a Chebyshev type I filterChebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
, with ripple factor ε
- Since the Butterworth filter is a limiting form of the Chebyshev filter, it follows that in the limit of
, 
and 
such that 
the filter becomes a Butterworth filterButterworth filterThe Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
- In the limit of
, 
and 
such that 
and 
, the filter becomes a Chebyshev type II filterChebyshev filterChebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
with gain
Poles and zeroes
Elliptic rational functions
In mathematics the elliptic rational functions are a sequence of rational functions with real coefficients. Elliptic rational functions are extensively used in the design of elliptic electronic filters...
.
The poles of the gain of an elliptic filter may be derived in a manner very similar to the derivation of the poles of the gain of a type I Chebyshev filter
Chebyshev filter
Chebyshev filters are analog or digital filters having a steeper roll-off and more passband ripple or stopband ripple than Butterworth filters...
. For simplicity, assume that the cutoff frequency is equal to unity. The poles
of the gain of the elliptical filter will be the zeroes of the denominator of the gain. Using the complex frequency this means that:Defining
where cd is the Jacobi elliptic cosine function and using the definition of the elliptic rational functions yields:where
and . Solving for wwhere the multiple values of the inverse cd function are made explicit using the integer index m.
The poles of the elliptic gain function are then:
As is the case for the Chebyshev polynomials, this may be expressed in explicitly complex form
where
is a function of and and are the zeroes of the elliptic rational function. is expressible for all n in terms of Jacobi elliptic functions, or algebraically for some orders, especially orders 1,2, and 3. For orders 1 and 2 we havewhere
The algebraic expression for
is rather involved (See ).The nesting property of the elliptic rational functions
Elliptic rational functions
In mathematics the elliptic rational functions are a sequence of rational functions with real coefficients. Elliptic rational functions are extensively used in the design of elliptic electronic filters...
can be used to build up higher order expressions for
:where
.Minimum Q-factor elliptic filters
Elliptic filters are generally specified by requiring a particular value for the passband ripple, stopband ripple and the sharpness of the cutoff. This will generally specify a minimum value of the filter order which must be used. Another design consideration is the sensitivity of the gain function to the values of the electronic components used to build the filter. This sensitivity is inversely proportional to the quality factor (Q-factor) of the poles of the transfer function of the filter. The Q-factor of a pole is defined as:
and is a measure of the influence of the pole on the gain function. For an elliptic filter, it happens that, for a given order, there exists a relationship between the ripple factor and selectivity factor which simultaneously minimizes the Q-factor of all poles in the transfer function:
This results in a filter which is maximally insensitive to component variations, but the ability to independently specify the passband and stopband ripples will be lost. For such filters, as the order increases, the ripple in both bands will decrease and the rate of cutoff will increase. If one decides to use a minimum-Q elliptic filter in order to achieve a particular minimum ripple in the filter bands along with a particular rate of cutoff, the order needed will generally be greater than the order one would otherwise need without the minimum-Q restriction. An image of the absolute value of the gain will look very much like the image in the previous section, except that the poles are arranged in a circle rather than an ellipse. They will not be evenly spaced and there will be zeroes on the ω axis, unlike the Butterworth filter
Butterworth filter
The Butterworth filter is a type of signal processing filter designed to have as flat a frequency response as possible in the passband so that it is also termed a maximally flat magnitude filter...
, whose poles are also arranged in a circle.
Comparison with other linear filters
Here is an image showing the elliptic filter next to other common kind of filters obtained with the same number of coefficients: