Elementary class
Encyclopedia
In the branch of mathematical logic
called model theory
, an elementary class (or axiomatizable class) is a class
consisting of all structures
satisfying a fixed first-order
theory
.
K of structures
of a signature
σ is called an elementary class if there is a first-order
theory
T of signature σ, such that K consists of all models of T, i.e., of all σ-structures that satisfy T. If T can be chosen as a theory consisting of a single first-order sentence, then K is called a basic elementary class.
More generally, K is a pseudo-elementary class
if there is a first-order theory T of a signature that extends σ, such that K consists of all σ-structures that are reduct
s to σ of models of T. In other words, a class K of σ-structures is pseudo-elementary iff
there is an elementary class K' such that K consists of precisely the reducts to σ of the structures in K' .
For obvious reasons, elementary classes are also called axiomatizable in first-order logic, and basic elementary classes are called finitely axiomatizable in first-order logic. These definitions extend to other logics in the obvious way, but since the first-order case is by far the most important, axiomatizable implicitly refers to this case when no other logic is specified.
, the slightly different earlier definitions are still in use in finite model theory
, where an elementary class may be called a Δ-elementary class, and the terms elementary class and first-order axiomatizable class are reserved for basic elementary classes (Ebbinghaus et al. 1994, Ebbinghaus and Flum 2005). Hodges calls elementary classes axiomatizable classes, and he refers to basic elementary classes as definable classes. He also uses the respective synonyms EC class and EC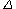
class (Hodges, 1993).
There are good reasons for this diverging terminology. The signature
s that are considered in general model theory are often infinite, while a single first-order
sentence
contains only finitely many symbols. Therefore basic elementary classes are atypical in infinite model theory. Finite model theory, on the other hand, deals almost exclusively with finite signatures. It is easy to see that for every finite signature σ and for every class K of σ-structures closed under isomorphism there is an elementary class
of σ-structures such that K and 
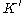contain precisely the same finite structures. Hence elementary classes are not very interesting for finite model theorists.
, a class of σ-structures is basic elementary if and only if it is elementary and its complement is also elementary.
symbol f. The class K of σ-structures in which f is one-to-one is a basic elementary class. This is witnessed by the theory T, which consists only of the single sentence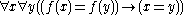
.
"
",
"
",
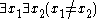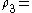and so on. (So the sentence
says that there are at least n elements.) The infinite σ-structures are precisely the models of the theory
.
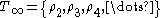But K is not a basic elementary class. Otherwise the infinite σ-structures would be precisely those that satisfy a certain first-order sentence τ. But then the set
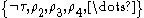would be inconsistent. By the compactness theorem
, for some natural number n the set
would be inconsistent. But this is absurd, because this theory is satisfied by any σ-structure with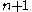 
or more elements.
However, there is a basic elementary class K' in the signature σ' = σ 
{f}, where f is a unary function symbol, such that K consists exactly of the reducts to σ of σ'-structures in K' . K' is axiomatised by the single sentence 
, which expresses that f is injective but not surjective. Therefore K is elementary and what could be called basic pseudo-elementary, but not basic elementary.
into two subsets: Those elements for which P holds, and the rest. Let K be the class of all σ-structures for which these two subsets have the same cardinality, i.e., there is a bijection between them. This class is not elementary, because a σ-structure in which both the set of realisations of P and its complement are countably infinite satisfies precisely the same first-order sentences as a σ-structure in which one of the sets is countably infinite and the other is uncountable.
Now consider the signature
, which consists of P along with a unary function symbol f. Let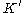 
be the class of all 
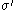-structures such that f is a bijection and P holds for x iff
P does not hold for f(x).
is clearly an elementary class, and therefore K is an example of a pseudo-elementary class that is not elementary.
This example demonstrates the limits of expressive power inherent in first-order logic
as opposed to the far more expressive second-order logic
. Second-order logic, however, fails to retain many desirable properties of first-order logic, such as the compactness theorem.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
called model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, an elementary class (or axiomatizable class) is a class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
consisting of all structures
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
satisfying a fixed first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
.
Definition
A classClass (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
K of structures
Structure (mathematical logic)
In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....
of a signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
σ is called an elementary class if there is a first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
T of signature σ, such that K consists of all models of T, i.e., of all σ-structures that satisfy T. If T can be chosen as a theory consisting of a single first-order sentence, then K is called a basic elementary class.
More generally, K is a pseudo-elementary class
Pseudoelementary class
In logic, a pseudoelementary class is a class of structures derived from an elementary class by omitting some of its sorts and relations. It is the mathematical logic counterpart of the notion in category theory of a forgetful functor, and in physics of hidden variable theories purporting to...
if there is a first-order theory T of a signature that extends σ, such that K consists of all σ-structures that are reduct
Reduct
In universal algebra and in model theory, a reduct of an algebraic structure is obtained by omitting some of the operations and relations of that structure...
s to σ of models of T. In other words, a class K of σ-structures is pseudo-elementary iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
there is an elementary class K
For obvious reasons, elementary classes are also called axiomatizable in first-order logic, and basic elementary classes are called finitely axiomatizable in first-order logic. These definitions extend to other logics in the obvious way, but since the first-order case is by far the most important, axiomatizable implicitly refers to this case when no other logic is specified.
Conflicting and alternative terminology
While the above is nowadays standard terminology in "infinite" model theoryModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, the slightly different earlier definitions are still in use in finite model theory
Finite model theory
Finite Model Theory is a subarea of model theory . MT is the branch of mathematical logic which deals with the relation between a formal language and its interpretations . FMT is a restriction of MT to interpretations of finite structures, i.e...
, where an elementary class may be called a Δ-elementary class, and the terms elementary class and first-order axiomatizable class are reserved for basic elementary classes (Ebbinghaus et al. 1994, Ebbinghaus and Flum 2005). Hodges calls elementary classes axiomatizable classes, and he refers to basic elementary classes as definable classes. He also uses the respective synonyms EC class and EC
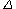class (Hodges, 1993).There are good reasons for this diverging terminology. The signature
Signature (logic)
In logic, especially mathematical logic, a signature lists and describes the non-logical symbols of a formal language. In universal algebra, a signature lists the operations that characterize an algebraic structure. In model theory, signatures are used for both purposes.Signatures play the same...
s that are considered in general model theory are often infinite, while a single first-order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
sentence
Sentence (mathematical logic)
In mathematical logic, a sentence of a predicate logic is a boolean-valued well formed formula with no free variables. A sentence can be viewed as expressing a proposition, something that may be true or false...
contains only finitely many symbols. Therefore basic elementary classes are atypical in infinite model theory. Finite model theory, on the other hand, deals almost exclusively with finite signatures. It is easy to see that for every finite signature σ and for every class K of σ-structures closed under isomorphism there is an elementary class
of σ-structures such that K and 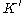contain precisely the same finite structures. Hence elementary classes are not very interesting for finite model theorists.Easy relations between the notions
Clearly every basic elementary class is an elementary class, and every elementary class is a pseudo-elementary class. Moreover, as an easy consequence of the compactness theoremCompactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
, a class of σ-structures is basic elementary if and only if it is elementary and its complement is also elementary.
A basic elementary class
Let σ be a signature consisting only of a unary functionUnary function
A unary function is a function that takes one argument. In computer science, a unary operator is a subset of unary function.Many of the elementary functions are unary functions, in particular the trigonometric functions and hyperbolic function are unary....
symbol f. The class K of σ-structures in which f is one-to-one is a basic elementary class. This is witnessed by the theory T, which consists only of the single sentence
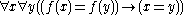.An elementary, basic pseudoelementary class that is not basic elementary
Let σ be an arbitrary signature. The class K of all infinite σ-structures is elementary. To see this, consider the sentences ""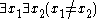, "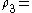",and so on. (So the sentence
says that there are at least n elements.) The infinite σ-structures are precisely the models of the theory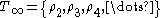.But K is not a basic elementary class. Otherwise the infinite σ-structures would be precisely those that satisfy a certain first-order sentence τ. But then the set
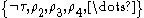would be inconsistent. By the compactness theoremCompactness theorem
In mathematical logic, the compactness theorem states that a set of first-order sentences has a model if and only if every finite subset of it has a model...
, for some natural number n the set
would be inconsistent. But this is absurd, because this theory is satisfied by any σ-structure with 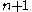or more elements.However, there is a basic elementary class K
{f}, where f is a unary function symbol, such that K consists exactly of the reducts to σ of σ'-structures in K, which expresses that f is injective but not surjective. Therefore K is elementary and what could be called basic pseudo-elementary, but not basic elementary.Pseudo-elementary class that is non-elementary
Finally, consider the signature σ consisting of a single unary relation symbol P. Every σ-structure is partitionedPartition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
into two subsets: Those elements for which P holds, and the rest. Let K be the class of all σ-structures for which these two subsets have the same cardinality, i.e., there is a bijection between them. This class is not elementary, because a σ-structure in which both the set of realisations of P and its complement are countably infinite satisfies precisely the same first-order sentences as a σ-structure in which one of the sets is countably infinite and the other is uncountable.
Now consider the signature
, which consists of P along with a unary function symbol f. Let 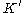be the class of all 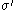-structures such that f is a bijection and P holds for x iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
P does not hold for f(x).
is clearly an elementary class, and therefore K is an example of a pseudo-elementary class that is not elementary.Non-pseudo-elementary class
Let σ be an arbitrary signature. The class K of all finite σ-structures is not elementary, because (as shown above) its complement is elementary but not basic elementary. Since this is also true for every signature extending σ, K is not even a pseudo-elementary class.This example demonstrates the limits of expressive power inherent in first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
as opposed to the far more expressive second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
. Second-order logic, however, fails to retain many desirable properties of first-order logic, such as the compactness theorem.