Ekeland's variational principle
Encyclopedia
In mathematical analysis
, Ekeland's variational principle, discovered by Ivar Ekeland
, is a theorem that asserts that there exists nearly optimal solutions to some optimization problem
s.
Ekeland's variational principle can be used when the lower level set
of a minimization problems is not compact, so that the Bolzano–Weierstrass theorem can not be applied. Ekeland's principle relies on the completeness
of the metric space
.
Ekeland's principle leads to a quick proof of the Caristi fixed point theorem
.
Ekeland was associated with the Paris Dauphine University when he proposed this theorem.
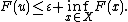
Then there exists a point v ∈ X such that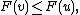
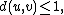
and, for all w ≠ v,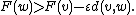
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, Ekeland's variational principle, discovered by Ivar Ekeland
Ivar Ekeland
Ivar Ekeland is a French mathematician of Norwegian descent. Ekeland has written influential monographs and textbooks on nonlinear functional analysis, the calculus of variations, and mathematical economics, as well as popular books on mathematics, which have been published in French, English, and...
, is a theorem that asserts that there exists nearly optimal solutions to some optimization problem
Optimization problem
In mathematics and computer science, an optimization problem is the problem of finding the best solution from all feasible solutions. Optimization problems can be divided into two categories depending on whether the variables are continuous or discrete. An optimization problem with discrete...
s.
Ekeland's variational principle can be used when the lower level set
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
of a minimization problems is not compact, so that the Bolzano–Weierstrass theorem can not be applied. Ekeland's principle relies on the completeness
Completeness
In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.-Logical completeness:In logic, semantic completeness is the converse of soundness for formal systems...
of the metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
.
Ekeland's principle leads to a quick proof of the Caristi fixed point theorem
Caristi fixed point theorem
In mathematics, the Caristi fixed-point theorem generalizes the Banach fixed point theorem for maps of a complete metric space into itself. Caristi's fixed-point theorem is a variation of the ε-variational principle of Ekeland...
.
Ekeland was associated with the Paris Dauphine University when he proposed this theorem.
Statement of the theorem
Let (X, d) be a complete metric space, and let F: X → R ∪ {+∞} be a lower semicontinuous functional on X that is bounded below and not identically equal to +∞. Fix ε > 0 and a point u ∈ X such that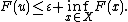
Then there exists a point v ∈ X such that
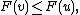
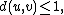
and, for all w ≠ v,