
Caristi fixed point theorem
Encyclopedia
In mathematics
, the Caristi fixed-point theorem (also known as the Caristi–Kirk fixed-point theorem) generalizes the Banach fixed point theorem
for maps of a complete
metric space
into itself. Caristi's fixed-point theorem is a variation of the ε-variational principle of
Ekeland
(1974, 1979). Moreover, the conclusion of Caristi's theorem is equivalent to metric completeness, as proved by Weston (1977). The original result is due to the mathematicians James Caristi and William Arthur Kirk
.
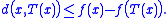
Then T has a fixed point in X, i.e. a point x0 such that T(x0) = x0.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Caristi fixed-point theorem (also known as the Caristi–Kirk fixed-point theorem) generalizes the Banach fixed point theorem
Banach fixed point theorem
In mathematics, the Banach fixed-point theorem is an important tool in the theory of metric spaces; it guarantees the existence and uniqueness of fixed points of certain self-maps of metric spaces, and provides a constructive method to find those fixed points...
for maps of a complete
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
into itself. Caristi's fixed-point theorem is a variation of the ε-variational principle of
Ekeland's variational principle
In mathematical analysis, Ekeland's variational principle, discovered by Ivar Ekeland, is a theorem that asserts that there exists nearly optimal solutions to some optimization problems....
Ekeland
Ivar Ekeland
Ivar Ekeland is a French mathematician of Norwegian descent. Ekeland has written influential monographs and textbooks on nonlinear functional analysis, the calculus of variations, and mathematical economics, as well as popular books on mathematics, which have been published in French, English, and...
(1974, 1979). Moreover, the conclusion of Caristi's theorem is equivalent to metric completeness, as proved by Weston (1977). The original result is due to the mathematicians James Caristi and William Arthur Kirk
William Arthur Kirk
William Arthur Kirk is an American mathematician. His research interests include nonlinear functional analysis, the geometry of Banach spaces and metric spaces. In particular, he has made notable contributions to the fixed point theory of metric spaces; for example, he is one of the two namesakes...
.
Statement of the theorem
Let (X, d) be a complete metric space. Let T : X → X and f : X → [0, +∞) be a lower semicontinuous function from X into the non-negative real numbers. Suppose that, for all points x in X,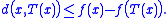
Then T has a fixed point in X, i.e. a point x0 such that T(x0) = x0.

