
Eells–Kuiper manifold
Encyclopedia
In mathematics, Eells–Kuiper manifold is a compactification
of by an
by an  - sphere
- sphere
, where n = 2, 4, 8, or 16.
If n = 2, the Eells–Kuiper manifold is diffeomorphic
to the real projective plane
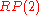 . For
. For  it is simply-connected
it is simply-connected
and has the integral cohomology structure of the complex projective plane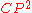 (
( ), of the quaternionic projective plane
), of the quaternionic projective plane
 (
( ) or of the Cayley projective plane (n = 16).
) or of the Cayley projective plane (n = 16).
and foliation theory
:
Theorem: Let be a connected
be a connected
closed
manifold
(not necessarily orientable) of dimension . Suppose
. Suppose  admits a Morse function
admits a Morse function 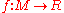 of class
of class 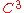 with exactly three singular points
with exactly three singular points
. Then is a Eells–Kuiper manifold.
is a Eells–Kuiper manifold.
Theorem: Let be a compact connected manifold and
be a compact connected manifold and  a Morse foliation on
a Morse foliation on  . Suppose the number of centers
. Suppose the number of centers  of the foliation
of the foliation  is more than the number of saddle
is more than the number of saddle
s . Then there are two possibilities:
. Then there are two possibilities:
Compactification
Compactification may refer to:* Compactification , making a topological space compact* Compactification , the "curling up" of extra dimensions in string theory* Compaction...
of
 by an
by an  - sphere
- sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, where n = 2, 4, 8, or 16.
If n = 2, the Eells–Kuiper manifold is diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
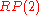 . For
. For  it is simply-connected
it is simply-connectedSimply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
and has the integral cohomology structure of the complex projective plane
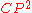 (
( ), of the quaternionic projective plane
), of the quaternionic projective planeQuaternionic projective space
In mathematics, quaternionic projective space is an extension of the ideas of real projective space and complex projective space, to the case where coordinates lie in the ring of quaternions H. Quaternionic projective space of dimension n is usually denoted byand is a closed manifold of dimension 4n...
 (
( ) or of the Cayley projective plane (n = 16).
) or of the Cayley projective plane (n = 16).Properties
These manifolds are important in both Morse theoryMorse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
and foliation theory
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
:
Theorem: Let
 be a connected
be a connectedConnection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(not necessarily orientable) of dimension
 . Suppose
. Suppose  admits a Morse function
admits a Morse function 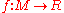 of class
of class 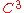 with exactly three singular points
with exactly three singular pointsCritical point
Critical point may refer to:*Critical point *Critical point *Critical point *Construction point of a ski jumping hill-See also:*Brillouin zone*Percolation thresholds...
. Then
 is a Eells–Kuiper manifold.
is a Eells–Kuiper manifold.Theorem: Let
 be a compact connected manifold and
be a compact connected manifold and  a Morse foliation on
a Morse foliation on  . Suppose the number of centers
. Suppose the number of centers  of the foliation
of the foliation  is more than the number of saddle
is more than the number of saddleSaddle
A saddle is a supportive structure for a rider or other load, fastened to an animal's back by a girth. The most common type is the equestrian saddle designed for a horse, but specialized saddles have been created for camels and other creatures...
s
 . Then there are two possibilities:
. Then there are two possibilities:-
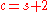 , and
, and 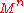 is homeomorphic to the sphere
is homeomorphic to the sphere 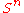 ,
,
-
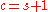 , and
, and 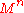 is an Eells—Kuiper manifold,
is an Eells—Kuiper manifold,  or
or 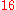 .
.

